题目内容
4.当-1≤x≤2时,二次函数y=(x-m)2+m2有最小值3,则实数m的值为$\frac{-1-\sqrt{5}}{2}$或$\sqrt{3}$.分析 根据二次函数的最值问题列出方程求出m的值,再根据二次项系数大于0解答.
解答 解:∵二次函数y=(x-m)2+m2有最小值3,
二次项系数a=1>0,故图象开口向上,对称轴为x=m,
当m<-1时,最小值在x=-1取得,此时有(m+1)2+m2=3,
求得m=$\frac{-1±\sqrt{5}}{2}$,
∵m<-1,
∴m=$\frac{-1-\sqrt{5}}{2}$;
当-1≤m≤2时,最小值在x=m时取得,即有1-m2=-2
求得m=$\sqrt{3}$或m=-$\sqrt{3}$(舍去)
当m>2时,最小值在x=2时取得,即(2-m)2+m2=3
求得m=$\frac{2±\sqrt{2}}{2}$(舍去)
故答案为:$\frac{-1-\sqrt{5}}{2}$或$\sqrt{3}$.
点评 本题考查了二次函数的最值问题,要注意二次函数有最小值,二次项系数大于0.

练习册系列答案
相关题目
14.下列各数中,是无理数的是( )
| A. | -$\sqrt{4}$ | B. | 3.14 | C. | $\frac{1}{7}$ | D. | $\frac{π}{2}$ |
 如图,现在甲、乙、丙三家公司共建一个污水处理站,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)
如图,现在甲、乙、丙三家公司共建一个污水处理站,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)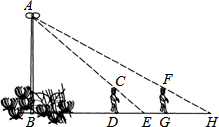 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.