题目内容
20.已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车或火车中的一种进行运输,且须提前预订,现有货运收费项目及收费村准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下: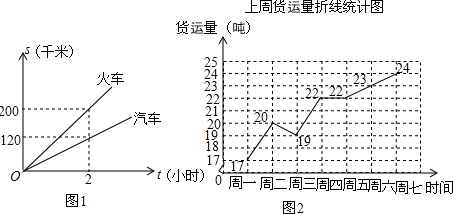
货运收费项目及收费标准表
| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |
(2)设每于用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、y火与x的函数关系式(不必写出x的取值范围),及x为何值时y汽>y火(总费用=运输费+冷藏费+固定费用);
(3)根据上周货运量的折线统计图,请你从平均数和折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
分析 (1)根据点的坐标为:(2,120),(2,200),直接得出两车的速度即可;
(2)根据图表得出货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象,得出关系式即可;
(3)根据平均数的求法以及折线图走势两个角度分析得出运输总费用较省方案.
解答 解:(1)根据图表上点的坐标为:(2,120),(2,200),
∴汽车的速度为 60千米/时,火车的速度为 100千米/时.
故答案为:60千米/时,100千米/时;
(2)依据题意得出:
y 汽=240×2x+$\frac{240}{60}$×5x+200,
=500x+200;
y 火=240×1.6x+$\frac{240}{100}$×5x+2280,
=396x+2280.
若y 汽>y 火,得出500x+200>396x+2280.
∴x>20;
(3)上周货运量$\overline{x}$=(17+20+19+22+22+23+24)÷7=21>20,
从平均数分析,建议预定火车费用较省.
从折线图走势分析,上周货运量周四(含周四)后大于20且呈上升趋势,建议预订火车费用较省
点评 此题主要考查了一次函数的应用以及折线图走势,根据数形结合解决实际问题是解决问题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
10.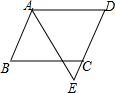 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
 如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交DC的延长线于点E,CE的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 2.5 |
15.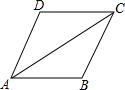 如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )
如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )
 如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )
如图,菱形ABCD中,已知∠D=110°,则∠BAC的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
5.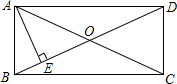 如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )
如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )
 如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )
如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )| A. | 67.5° | B. | 45° | C. | 22.5° | D. | 无法确定 |