题目内容
20.计算:(1)${({-2\sqrt{\frac{3}{2}}})^2}$
(2)$({-3\sqrt{\frac{1}{27}}})({-\frac{1}{2}\sqrt{12}})$
(3)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$
(4)6-2$\sqrt{\frac{3}{2}}-3\sqrt{\frac{3}{2}}$.
分析 (1)利用二次根式的性质计算;
(2)利用二次根式的乘法法则计算;
(3)先把各二次根式化为最简二次根式,然后合并即可;
(4)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=4×$\frac{3}{2}$
=6;
(2)原式=-3×(-$\frac{1}{2}$)×$\sqrt{\frac{1}{27}×12}$
=$\frac{3}{2}$×$\frac{2}{3}$
=1;
(3)原式=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
(4)原式=6-$\sqrt{6}$-$\frac{3\sqrt{6}}{2}$
=6-$\frac{5\sqrt{6}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 已知:如图,四边形ABCD、EBNM都是正方形,且sinα=$\frac{5}{13}$,求tanβ的值.
已知:如图,四边形ABCD、EBNM都是正方形,且sinα=$\frac{5}{13}$,求tanβ的值.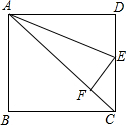 如图,已知正方形ABCD的边长为1,以AE为折痕使点D落在AC上F处,求DE的长.
如图,已知正方形ABCD的边长为1,以AE为折痕使点D落在AC上F处,求DE的长.