题目内容
11. 如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)
如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)(1)求长方体底面的对角线长.
(2)若揭开盖子EFGH后,捕入一根长为10cm的细木棒,则细木棒露在外面的最短长度是多少?
分析 (1)根据勾股定理求出盒子底面对角长即可;
(2)长方体内体对角线是最长的,当木条在盒子里对角放置的时候露在外面的长度最小,根据勾股定理求出长方体纸箱的对角线长度,再用细木棒的长度减去长方体纸箱的对角线长度即可.
解答 解:(1)$\sqrt{{3}^{2}+{4}^{2}}$=5(cm).
答:长方体底面的对角线长是5cm.
(2)$\sqrt{{5}^{2}+{6}^{2}}$=$\sqrt{61}$(cm),
细木棒露在外面的最短长度是(10-$\sqrt{61}$)cm.
点评 本题重点考查学生的空间想象能力及勾股定理的应用.解题的关键是熟悉勾股定理并两次应用勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
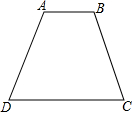 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=6,点P在线段AD上,满足条件∠BPC=90°的点P有且只有一个,则等腰梯形ABCD的面积是18.
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=6,点P在线段AD上,满足条件∠BPC=90°的点P有且只有一个,则等腰梯形ABCD的面积是18.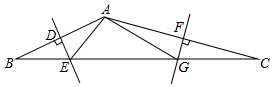 如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7.
如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7.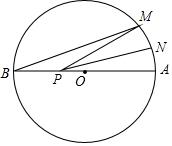 如图,AB是⊙O的直径,AB=6,点M在⊙O上,∠MBA=20°,N是$\widehat{MA}$的中点,P是直径AB上的一动点,若AN=1,则△PMN周长的最小值为( )
如图,AB是⊙O的直径,AB=6,点M在⊙O上,∠MBA=20°,N是$\widehat{MA}$的中点,P是直径AB上的一动点,若AN=1,则△PMN周长的最小值为( )