题目内容
6.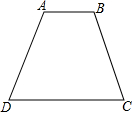 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=6,点P在线段AD上,满足条件∠BPC=90°的点P有且只有一个,则等腰梯形ABCD的面积是18.
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=6,点P在线段AD上,满足条件∠BPC=90°的点P有且只有一个,则等腰梯形ABCD的面积是18.
分析 如图,当以BC为直径的⊙O与直线AD相切于点P时,满足条件∠BPC=90°的点P有且只有一个.连接PB、PC、OP、OD、OA延长AO交DC的延长线于E.由△ABO≌△ECO,推出S△ABO=S△EOC,OA=OE,推出S梯形ABCD=S△ADE=2S△AOD即可解决问题.
解答 解:如图,当以BC为直径的⊙O与直线AD相切于点P时,满足条件∠BPC=90°的点P有且只有一个.连接PB、PC、OP、OD、OA延长AO交DC的延长线于E.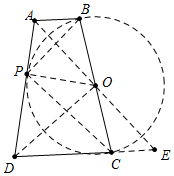
∵OP⊥AD,OP=OB=OC=3,
∴S△AOD=$\frac{1}{2}$•AD•OP=$\frac{1}{2}$×6×3=9,
∵AB∥DE,
∴∠BAO=∠E,
在△ABO和△ECO中,
$\left\{\begin{array}{l}{∠BAO=∠E}\\{∠AOB=∠EOC}\\{BO=OC}\end{array}\right.$,
∴△ABO≌△ECO,
∴S△ABO=S△EOC,OA=OE,
∴S梯形ABCD=S△ADE=2S△AOD=18.
故答案为18.
点评 本题考查梯形的性质、直径所对的圆周角是直角、全等三角形的判定和性质、切线的性质等知识,解题的关键是学会添加常用辅助线,确定点P的位置,学会用转化的思想思考问题,属于中考填空题中的压轴题.

练习册系列答案
相关题目
14.计算(-2a)2•a3,正确的是( )
| A. | 2a5 | B. | -4a5 | C. | 4a5 | D. | 4a6 |
15.在线段AB上取一点C,使AC=$\frac{1}{3}$AB,再在线段AB的延长线上取一点D,使DB=$\frac{1}{4}$AD,则线段BC的长度是线段DC长度的( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
16. 如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )
如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )
 如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )
如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )| A. | 17.5° | B. | 35° | C. | 60° | D. | 70° |
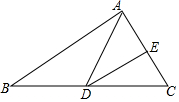 已知D、E分别是△ABC的边BC和边AC的中点,连接DE、AD,若S△ABC=24cm2,则S△DEC=6cm2.
已知D、E分别是△ABC的边BC和边AC的中点,连接DE、AD,若S△ABC=24cm2,则S△DEC=6cm2. 如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)
如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)