题目内容
3.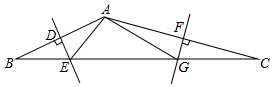 如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7.
如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7.
分析 由题意知,DE、FG分别是边AB、AC的垂直平分线,根据线段垂直平分线的性质,可得,BE=AE,AG=GC,又C△AEG=AE+AG+EG,BC=8,所以,代入即可得出.
解答 解:如图.
∵DE、FG分别是边AB、AC的垂直平分线,
∴BE=AE,AG=GC,
∴BE+GC=AE+AG,
∴C△AEG=AE+AG+EG,
=BE+GC+EG,
=BC,
又∵BC=7,
∴C△AEG=7.
故答案为:7.
点评 本题主要考查了线段垂直平分线的性质,熟练掌握线段垂直平分线上的点到两端点的距离相等.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
14.计算(-2a)2•a3,正确的是( )
| A. | 2a5 | B. | -4a5 | C. | 4a5 | D. | 4a6 |
8.下列计算错误的是( )
| A. | sin60°-sin30°=sin30° | B. | sin245°+cos245°=1 | ||
| C. | (tan60°)2=3 | D. | tan30°=$\frac{sin30°}{cos30°}$ |
15.在线段AB上取一点C,使AC=$\frac{1}{3}$AB,再在线段AB的延长线上取一点D,使DB=$\frac{1}{4}$AD,则线段BC的长度是线段DC长度的( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
13.如果a的倒数是-1,那么a2016=( )
| A. | 1 | B. | -1 | C. | 2016 | D. | -2016 |
 如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)
如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)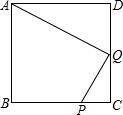 如图:正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点.
如图:正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点.