题目内容
19.写出等边三角形的面积S与其边长a之间的关系式,并分别计算当a=1,$\sqrt{3}$,2时三角形的面积.分析 根据三角形面积公式以及等边三角形的三线合一即可求出S与a的关系式.
解答 解:在等边三角形中,
底边上的高为:$\frac{\sqrt{3}}{2}$a,
∴S=$\frac{\sqrt{3}}{4}$a2,
当a=1时,
∴S=$\frac{\sqrt{3}}{4}$,
当a=$\sqrt{3}$时,
∴S=$\frac{\sqrt{3}}{4}$×3=$\frac{3\sqrt{3}}{4}$
当a=2时,
∴S=$\sqrt{3}$
点评 本题考查函数关系,解题的关键是根据等边三角形的性质求出底边上的高,本题属于基础题型.

练习册系列答案
相关题目
14.计算(-2a)2•a3,正确的是( )
| A. | 2a5 | B. | -4a5 | C. | 4a5 | D. | 4a6 |
8.下列计算错误的是( )
| A. | sin60°-sin30°=sin30° | B. | sin245°+cos245°=1 | ||
| C. | (tan60°)2=3 | D. | tan30°=$\frac{sin30°}{cos30°}$ |
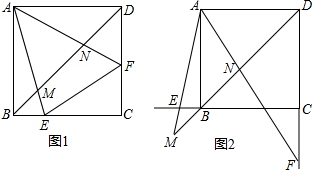
 如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)
如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(纸箱厚度忽略不计)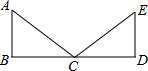 如图,AB⊥BD,AB∥ED,AC=EC,要证明△ABC≌△EDC,若以“AAS”为依据,还要添加一个条件为∠A=∠E(或∠ACB=∠ECD).
如图,AB⊥BD,AB∥ED,AC=EC,要证明△ABC≌△EDC,若以“AAS”为依据,还要添加一个条件为∠A=∠E(或∠ACB=∠ECD).