题目内容
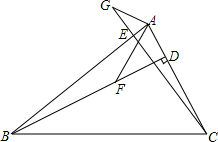 已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.
已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.求证:AG⊥AF.
考点:全等三角形的判定与性质
专题:证明题
分析:根据垂直求出∠BEO=∠CDO=90°,根据三角形的内角和定理求出∠ABF=∠ACG,推出△ABF≌△GCA,根据全等三角形的性质得出∠G=∠BAF即可.
解答:证明:∵BD,CE是△ABC的高,
∴∠BEO=∠CDO=90°,
∵∠EOB=∠DOC,∠ABF+∠EOB+∠BEO=180°,∠ACG+∠CDO+∠DOC=180°,
∴∠ABF=∠ACG,
在△ABF和△GCA中,
,
∴△ABF≌△GCA,
∴∠G=∠BAF,
∵∠GEA=∠CEB=90°,
∴∠G+∠GAB=90°,
∴∠BAF+∠GAB=90°,
∴∠GAF=90°,
∴AG⊥AF.
∴∠BEO=∠CDO=90°,
∵∠EOB=∠DOC,∠ABF+∠EOB+∠BEO=180°,∠ACG+∠CDO+∠DOC=180°,
∴∠ABF=∠ACG,
在△ABF和△GCA中,
|
∴△ABF≌△GCA,
∴∠G=∠BAF,
∵∠GEA=∠CEB=90°,
∴∠G+∠GAB=90°,
∴∠BAF+∠GAB=90°,
∴∠GAF=90°,
∴AG⊥AF.
点评:本题考查了三角形的内角和定理和全等三角形的性质和判定的应用,解此题的关键是推出△ABF≌△GCA,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
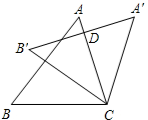 如图,将三角形△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )
如图,将三角形△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )| A、35° | B、65° |
| C、55° | D、25° |
在线段AB上选取3种点,第1种是将AB线段10等分的点;第2种是将AB线段12等分的点;第3种是将AB线段15等分的点,这些点连同AB线段的端点可组成线段的条数是( )
| A、350 | B、595 |
| C、666 | D、406 |
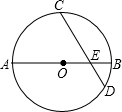 如图,⊙O的直径AB=8,点C为弧AB的中点,E为OB上一点,∠AEC=60°,CE的延长线交⊙O于D,求弦CD的长.
如图,⊙O的直径AB=8,点C为弧AB的中点,E为OB上一点,∠AEC=60°,CE的延长线交⊙O于D,求弦CD的长.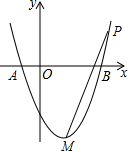 如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.
如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.



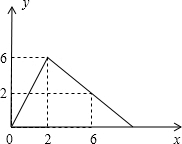 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后: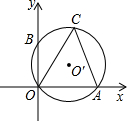 如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( )
如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( )