题目内容
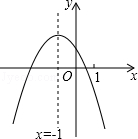 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④n(an+b)+b>a(n≠-1),
其中正确结论的个数是( )
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:二次函数图象与系数的关系
专题:计算题
分析:根据抛物线与x轴的交点个数可对①进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-2,0)与(-3,0)之间,则x=-2时,y>0,即4a-2b+c>0,则可对②进行判断;由抛物线的对称轴为直线x=-
=-1得到a=
,再利用x=1时,y<0得到a+b+c<0,则
+b+c<0,于是可对③进行判断;根据二次函数的最值问题得到an2+bn+c<a-b+c(n≠-1),即n(an+b)+b<a,则可对④进行判断.
| b |
| 2a |
| b |
| 2 |
| b |
| 2 |
解答:解:∵抛物线与x轴有2个交点,
∴b2-4ac>0,即4ac-b2<0,所以①正确;
∵抛物线与x轴的一个交点在(0,0)与(1,0)之间,
而抛物线的对称轴为直线x=-1,
∴抛物线与x轴的另一个交点在(-2,0)与(-3,0)之间,
∴x=-2时,y>0,
∴4a-2b+c>0,即4a+c>2b,所以②错误;
∵抛物线的对称轴为直线x=-
=-1,
∴a=
,
∵x=1时,y<0,
∴a+b+c<0,
∴
+b+c<0,即3b+2c<0,所以③正确;
∵x=-1时,函数值有最大值a-b+c,
∴an2+bn+c<a-b+c(n≠-1),
∴n(an+b)+b<a,所以④错误.
故选C.
∴b2-4ac>0,即4ac-b2<0,所以①正确;
∵抛物线与x轴的一个交点在(0,0)与(1,0)之间,
而抛物线的对称轴为直线x=-1,
∴抛物线与x轴的另一个交点在(-2,0)与(-3,0)之间,
∴x=-2时,y>0,
∴4a-2b+c>0,即4a+c>2b,所以②错误;
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴a=
| b |
| 2 |
∵x=1时,y<0,
∴a+b+c<0,
∴
| b |
| 2 |
∵x=-1时,函数值有最大值a-b+c,
∴an2+bn+c<a-b+c(n≠-1),
∴n(an+b)+b<a,所以④错误.
故选C.
点评:本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口,当a<0时,抛物线向下;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知A(-1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2-2x+m上,则y1、y2、y3的大小关系为( )
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
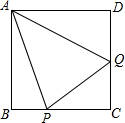 如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长.
如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长.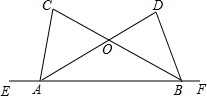 如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证:
如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证: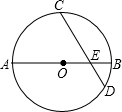 如图,⊙O的直径AB=8,点C为弧AB的中点,E为OB上一点,∠AEC=60°,CE的延长线交⊙O于D,求弦CD的长.
如图,⊙O的直径AB=8,点C为弧AB的中点,E为OB上一点,∠AEC=60°,CE的延长线交⊙O于D,求弦CD的长.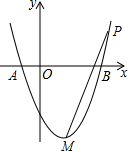 如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.
如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.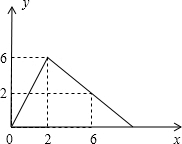 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后: 如图,AB是半圆O的直径,过⊙O上一点C,作CD⊥AB于点D.已知AC=3cm,BC=5cm,则AB=
如图,AB是半圆O的直径,过⊙O上一点C,作CD⊥AB于点D.已知AC=3cm,BC=5cm,则AB=