题目内容
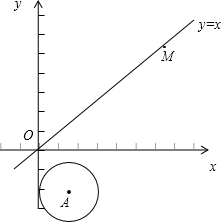 如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,-2)直线OM是一次函数y=x的图象,让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.
如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,-2)直线OM是一次函数y=x的图象,让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.(1)填空:
①直线OM与x轴所夹的锐角度数为
②当t=
(2)当t>3时,求出运动过程中⊙A与直线OM相切时t的值,
(3)运动过程中,当⊙A与直线OM相交所得的弦长为1时,求t的值.
考点:圆的综合题
专题:综合题
分析:(1)①利用直线y=x上点的坐标特征易得直线y=x为第一、三象限的角平分线,则直线OM与x轴所夹的锐角度数为45°;
②根据直线与圆的位置关系得到⊙A沿y轴正方向运动时,⊙A始终与y轴相切,所以当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点,易得t=1或t=2或t=3;
(2)作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,如图1,OB=t-2,AB=AC=1,OH=1,先判断△OPH和△APC都是等腰直角三角形,则PH=OH=1,AP=
AC=
,得到AH=AP+PH=
+1,然后利用AH=OB得到方程t-2=
+1,再解一次方程即可;
(3)分类讨论:当点A在x轴下方,如图2,作AB⊥y轴于B,AC⊥直线OM于C,交x轴于Q,AH⊥x轴于H,⊙A与直线OM交于E、F,AB=OH=1,AE=AF=1,OB=AH=2-t,先得到△AEF为等边三角形,则AC=
AE=
,与(2)一样可得△OCQ和△AHQ都是等腰直角三角形,则HG=AH=2-t,所以OQ=OH-HQ=t-1,AQ=
(2-t),于是得到CQ=
OQ=
(t-1),利用AC=CQ+AQ得到方程
(t-1)+
(2-t)=
,再解方程即可;当点A在x轴上方,如图3,作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于Q,⊙A与直线OM交于E、F,则AB=OH=1,AE=AF=1,OB=AH=t-2,同样可得△AEF为等边三角形,AC=
,△ACQ和△OHQ都是等腰直角三角形,则HQ=OH=1,AQ=
AC=
•
=
,然后利用AH=HQ+AQ得到方程t-2=1+
,再方程求出t即可.
②根据直线与圆的位置关系得到⊙A沿y轴正方向运动时,⊙A始终与y轴相切,所以当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点,易得t=1或t=2或t=3;
(2)作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,如图1,OB=t-2,AB=AC=1,OH=1,先判断△OPH和△APC都是等腰直角三角形,则PH=OH=1,AP=
| 2 |
| 2 |
| 2 |
| 2 |
(3)分类讨论:当点A在x轴下方,如图2,作AB⊥y轴于B,AC⊥直线OM于C,交x轴于Q,AH⊥x轴于H,⊙A与直线OM交于E、F,AB=OH=1,AE=AF=1,OB=AH=2-t,先得到△AEF为等边三角形,则AC=
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:解:(1)①∵直线y=x上点到x轴和y轴的距离相等,
∴直线y=x为第一、三象限的角平分线,
∴直线OM与x轴所夹的锐角度数为45°;
②∵⊙A的半径为1,圆心A点的坐标为(1,-2),
∴⊙A沿y轴正方向运动时,⊙A始终与y轴相切,
当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点,
⊙A与x轴相切,则点A与x轴的距离为1,得到t=1或3;当点A在x轴上,则t=2;
所以t=1s或t=2或t=3;
故答案为45,1s或2s或3s;
(2)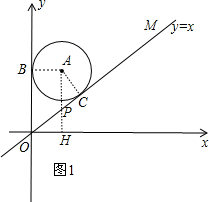 作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,如图1,
作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,如图1,
则OB=t-2,AB=AC=1,OH=1,
∵直线OM与x轴所夹的锐角度数为45°,
∴∠POH=45°,
∴∠OPH=45°,
∴∠APC=45°,
∴△OPH和△APC都是等腰直角三角形,
∴PH=OH=1,AP=
AC=
,
∴AH=AP+PH=
+1,
而AH=OB,
∴t-2=
+1,
∴t=3+
;
(3)当点A在x轴下方,如图2,作AB⊥y轴于B,AC⊥直线OM于C,交x轴于Q,AH⊥x轴于H,⊙A与直线OM交于E、F,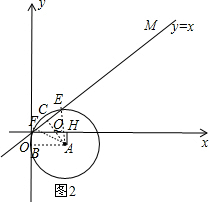
则AB=OH=1,AE=AF=1,OB=AH=2-t,
∵EF=1,
∴△AEF为等边三角形,
∴AC=
AE=
,
∵直线OM与x轴所夹的锐角度数为45°,
∴∠COH=45°,
与(2)一样可得△OCQ和△AHQ都是等腰直角三角形,
∴HQ=AH=2-t,
∴OQ=OH-HQ=t-1,AQ=
(2-t),
∴CQ=
OQ=
(t-1),
∵AC=CQ+AQ,
 ∴
∴
(t-1)+
(2-t)=
,解得t=3-
;
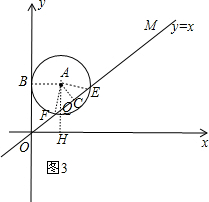
当点A在x轴上方,如图3,作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于Q,⊙A与直线OM交于E、F,
则AB=OH=1,AE=AF=1,OB=AH=t-2,
与前面一样可得△AEF为等边三角形,AC=
,△ACQ和△OHQ都是等腰直角三角形,
∵HQ=OH=1,AQ=
AC=
•
=
,
∵AH=HQ+AQ,
∴t-2=1+
,得t=3+
,
综上所述,t的值为3-
或3+
.
∴直线y=x为第一、三象限的角平分线,
∴直线OM与x轴所夹的锐角度数为45°;
②∵⊙A的半径为1,圆心A点的坐标为(1,-2),
∴⊙A沿y轴正方向运动时,⊙A始终与y轴相切,
当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点,
⊙A与x轴相切,则点A与x轴的距离为1,得到t=1或3;当点A在x轴上,则t=2;
所以t=1s或t=2或t=3;
故答案为45,1s或2s或3s;
(2)
 作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,如图1,
作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,如图1,则OB=t-2,AB=AC=1,OH=1,
∵直线OM与x轴所夹的锐角度数为45°,
∴∠POH=45°,
∴∠OPH=45°,
∴∠APC=45°,
∴△OPH和△APC都是等腰直角三角形,
∴PH=OH=1,AP=
| 2 |
| 2 |
∴AH=AP+PH=
| 2 |
而AH=OB,
∴t-2=
| 2 |
∴t=3+
| 2 |
(3)当点A在x轴下方,如图2,作AB⊥y轴于B,AC⊥直线OM于C,交x轴于Q,AH⊥x轴于H,⊙A与直线OM交于E、F,

则AB=OH=1,AE=AF=1,OB=AH=2-t,
∵EF=1,
∴△AEF为等边三角形,
∴AC=
| ||
| 2 |
| ||
| 2 |
∵直线OM与x轴所夹的锐角度数为45°,
∴∠COH=45°,
与(2)一样可得△OCQ和△AHQ都是等腰直角三角形,
∴HQ=AH=2-t,
∴OQ=OH-HQ=t-1,AQ=
| 2 |
∴CQ=
| ||
| 2 |
| ||
| 2 |
∵AC=CQ+AQ,
 ∴
∴
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
当点A在x轴上方,如图3,作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于Q,⊙A与直线OM交于E、F,
则AB=OH=1,AE=AF=1,OB=AH=t-2,
与前面一样可得△AEF为等边三角形,AC=
| ||
| 2 |
∵HQ=OH=1,AQ=
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∵AH=HQ+AQ,
∴t-2=1+
| ||
| 2 |
| ||
| 2 |
综上所述,t的值为3-
| ||
| 2 |
| ||
| 2 |
点评:本同考查了圆的综合题:熟练掌握切线的性质、垂径定理、等边三角形的判定与性质和等腰直角三角形的判定与性质;会运用分类讨论的思想解决数学问题;学会解决动点问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
[-8(a-3b)5(3a+b)6]÷[-2(a-3b)(3a+b)2]的计算结果为( )
| A、4(a-3b)4(3a+b)3 | ||
| B、-4(a-3b)5(3a+b)4 | ||
C、
| ||
| D、4(a-3b)4(3a+b)4 |
 如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,2),则∠ACO的度数是
如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,2),则∠ACO的度数是 如图,已知在△ABC中,DE∥BC,AD:DB=2:3,求:
如图,已知在△ABC中,DE∥BC,AD:DB=2:3,求: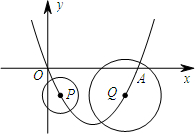 抛物线y=
抛物线y= 如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以对角线OB1为一边作正方形OB1B2C1,则B2的坐标是
如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以对角线OB1为一边作正方形OB1B2C1,则B2的坐标是