题目内容
 如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,2),则∠ACO的度数是
如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,2),则∠ACO的度数是考点:相似三角形的判定与性质,坐标与图形性质
专题:跨学科
分析:过B点作X轴的垂线与X轴相交于点D,由已知条件可以得到△OAC∽△DBC,从而得到OC和OA,CD,BD的数量关系,求出OC的长,进而求出∠ACO度数.
解答:解:过B点作X轴的垂线与X轴相交于点D,则BD⊥CD,

∵A点经过点C反射后经过B点,
∴∠OCA=∠DCB,
∴△OAC∽△DBC,
∴
=
,
∵A的坐标为(0,1),点B的坐标为(3,2),
∴OA=1,CD=OD-OC=3-OC,BD=2,
∴
=
,
∴OC=1,∴OA=OC,
∴∠ACO=45°.
故答案为45°.

∵A点经过点C反射后经过B点,
∴∠OCA=∠DCB,
∴△OAC∽△DBC,
∴
| OA |
| BD |
| OC |
| CD |
∵A的坐标为(0,1),点B的坐标为(3,2),
∴OA=1,CD=OD-OC=3-OC,BD=2,
∴
| 1 |
| 2 |
| OC |
| 2-OC |
∴OC=1,∴OA=OC,
∴∠ACO=45°.
故答案为45°.
点评:本题考查镜面反射的原理与性质、三角形相似的判定和性质,构造相似三角形是解决本题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,长方形OABC中,点D是OA的中点,点P在BC上运动,当△OPD是等腰三角形时,请你找出P点的位置.
如图,长方形OABC中,点D是OA的中点,点P在BC上运动,当△OPD是等腰三角形时,请你找出P点的位置.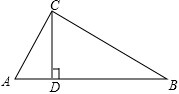 已知在△ABC中,CD⊥AB于D,由下列条件中的某一个就能推出△ABC是直角三角形的是
已知在△ABC中,CD⊥AB于D,由下列条件中的某一个就能推出△ABC是直角三角形的是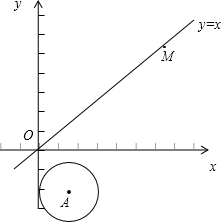 如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,-2)直线OM是一次函数y=x的图象,让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.
如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,-2)直线OM是一次函数y=x的图象,让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t. 如图,中间是一盏路灯,周围有一围栏杆,图(2)(3)表示的是这些栏杆的影子,但没有画完,请你把图(2)(3)补充完整.
如图,中间是一盏路灯,周围有一围栏杆,图(2)(3)表示的是这些栏杆的影子,但没有画完,请你把图(2)(3)补充完整.