题目内容
 如图,已知在△ABC中,DE∥BC,AD:DB=2:3,求:
如图,已知在△ABC中,DE∥BC,AD:DB=2:3,求:(1)△ADE与梯形BCED的面积比;
(2)△ADE和△ECB的面积比.
考点:相似三角形的判定与性质
专题:常规题型
分析:(1)根据题意可以判定△ADE∽△ABC,即可求得△ADE和△ABC的面积比,即可解题;
(2)根据△BDE中DE边上高和△ECB中BC边上的高相等即可求得△BDE和△ECB的面积比.
(2)根据△BDE中DE边上高和△ECB中BC边上的高相等即可求得△BDE和△ECB的面积比.
解答:解:(1)∵DE∥BC,AD:DB=2:3,
∴△ADE∽△ABC,且相似比为2:5,
∴△ADE和△ABC的面积比为4:25,
∴△ADE与梯形BCED的面积比为4:(25-4)=4:21;
(2)∵△BDE中DE边上高和△ECB中BC边上的高相等,
∴△BDE和△ECB的面积比为ED:BC=2:5;
∴△ADE和△ECB的面积比为4:(21×
)=4:15.
∴△ADE∽△ABC,且相似比为2:5,
∴△ADE和△ABC的面积比为4:25,
∴△ADE与梯形BCED的面积比为4:(25-4)=4:21;
(2)∵△BDE中DE边上高和△ECB中BC边上的高相等,
∴△BDE和△ECB的面积比为ED:BC=2:5;
∴△ADE和△ECB的面积比为4:(21×
| 5 |
| 7 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,考查了相似三角形面积比为相似比的平方的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
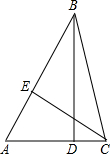 如图已知,△ABC中,∠ABC=45°,BD⊥AC于点D,CE⊥AB于点E,若BD=6,AD=3,求AC的长度.
如图已知,△ABC中,∠ABC=45°,BD⊥AC于点D,CE⊥AB于点E,若BD=6,AD=3,求AC的长度.
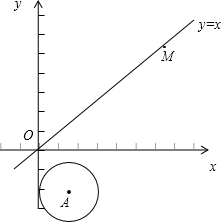 如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,-2)直线OM是一次函数y=x的图象,让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.
如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,-2)直线OM是一次函数y=x的图象,让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.