题目内容
18.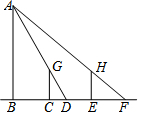 如图,王华晚上由路灯下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.求路灯A到直线CD的距离.
如图,王华晚上由路灯下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.求路灯A到直线CD的距离.
分析 设AB=x,先证明△DCG∽△DBA,利用相似比得到BC=$\frac{2x-3}{3}$,再证明△FEH∽△FBA,利用相似比得到$\frac{1.5}{x}$=$\frac{2}{2+3+1+\frac{2x-3}{3}}$,然后利用比例性质求出x即可.
解答 解:设AB=x,
∵GC∥AB,
∴△DCG∽△DBA,
∴$\frac{CG}{AB}=\frac{CD}{DB}$,即$\frac{1.5}{x}$=$\frac{1}{1+BC}$,
∴BC=$\frac{2x-3}{3}$,
∵HE∥AB,
∴△FEH∽△FBA,
∴$\frac{HE}{AB}$=$\frac{EF}{FB}$,即$\frac{1.5}{x}$=$\frac{2}{2+3+1+\frac{2x-3}{3}}$,解得x=7.5,
答:路灯A到直线CD的距离为7.5m.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.关于?ABCD的叙述,正确的是( )
| A. | 若AC⊥BD,则?ABCD是正方形 | B. | 若AC=BD,则?ABCD是正方形 | ||
| C. | 若AB⊥BC,则?ABCD是菱形 | D. | 若AB=BC,则?ABCD是菱形 |
7.在△ABC中,PA=PB=PC,则点P是△ABC( )
| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线交点 | D. | 三条角平分线的交点 |
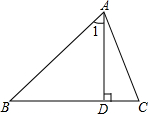 如图,AD是△ABC的高,∠1=∠B,∠C=65°,则∠BAC=70°.
如图,AD是△ABC的高,∠1=∠B,∠C=65°,则∠BAC=70°.