题目内容
9.在△ABC中,∠ACB=90°,AC=$\frac{1}{2}$AB=4cm,CD⊥AB于D,试判断以D为圆心,2$\sqrt{3}$cm为半径的⊙D与点A、B、C的位置关系.分析 根据直角三角形的性质,可得CD,AD,BD的长,根据d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内判断即可.
解答  解:∵∠ACB=90°,AC=$\frac{1}{2}$AB=4cm,
解:∵∠ACB=90°,AC=$\frac{1}{2}$AB=4cm,
∴AB=8cm,BC=4$\sqrt{3}$cm,∠B=30°,
∵CD⊥AB,
∴CD=$\frac{1}{2}$BC=2$\sqrt{3}$cm,
BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=6cm,AD=$\frac{1}{2}$AC=2cm,
∵CD=2$\sqrt{3}$cm,BD=6cm>2$\sqrt{3}$cm,AD=2cm<2$\sqrt{3}$cm,
∴以D为圆心,2$\sqrt{3}$cm为半径的⊙D与点A、B、C的位置关系是点C在⊙D上,点A在圆内,点B在圆外.
点评 本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.把一根绳子剪2次,正好剪成了3段,每段2米,则这根绳子原来长为( )
| A. | 6 | B. | 12 | C. | 14 | D. | 10 |
14.在直角三角形ABC中,∠C=60°,以AB为直径的半圆交斜边BC于D,则△ACD与△ABD的面积之比为( )
| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 3:4 |
1.从八边形的一个顶点出发可引出的对角线的条数有( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
19.若2axb3与-3a2by的和为单项式,则yx是( )
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
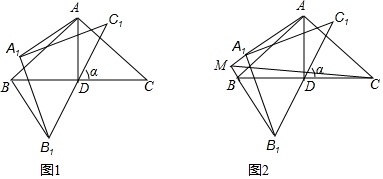
 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图: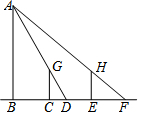 如图,王华晚上由路灯下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.求路灯A到直线CD的距离.
如图,王华晚上由路灯下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.求路灯A到直线CD的距离.