题目内容
如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
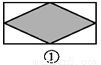
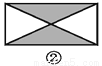
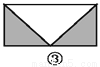
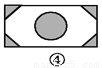
A. 4个 B. 3个 C. 2个 D. 1个
 A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A.
A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A.
练习册系列答案
相关题目
求cos42°,下列按键正确的是( )
A. 

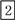
 B.
B. 


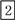

C. 


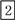 D.
D. 



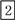
 A
【解析】试题解析:用计算器计算一个锐角的三角函数值的步骤,先三角函数,之后度数,最后等号;
故选A.
A
【解析】试题解析:用计算器计算一个锐角的三角函数值的步骤,先三角函数,之后度数,最后等号;
故选A. 点P是△ABC内任意一点,则∠APC与∠B的大小关系是 ( )
A. ∠APC>∠B B. ∠APC=∠B C. ∠APC<∠B D. 不能确定
 A
【解析】试题解析:
如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选A.
A
【解析】试题解析:
如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选A. 化简: 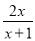 +
+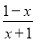 =___.
=___.
 1
【解析】分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可.
解答:【解析】
原式==1.
1
【解析】分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可.
解答:【解析】
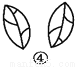
原式==1. 观察图①~④中的左右两个图形,它们是否成轴对称?如果是,请画出其对称轴.

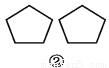
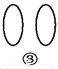
 见解析
【解析】判断两个图形是否成轴对称,关键是理解、应用两个图形成轴对称的定义,即看两个图形能否沿一条直线折叠后重合.若重合,则两个图形关于这条直线成轴对称,否则不成轴对称.
【解析】
图①②③中的左右两个图形成轴对称,题图④中的左右两个图形不成轴对称.
图①②③中成轴对称的两个图形的对称轴如图所示.
见解析
【解析】判断两个图形是否成轴对称,关键是理解、应用两个图形成轴对称的定义,即看两个图形能否沿一条直线折叠后重合.若重合,则两个图形关于这条直线成轴对称,否则不成轴对称.
【解析】
图①②③中的左右两个图形成轴对称,题图④中的左右两个图形不成轴对称.
图①②③中成轴对称的两个图形的对称轴如图所示. 在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.
 【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为: 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
 D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D.
D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D. 在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于 .
 .
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:.
.
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:. 用直尺和圆规作一个角的平分线如图所示,说明∠AOC=∠BOC的依据是( ).
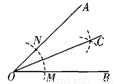
A. SSS B. ASA C. AAS D. 角平分线上的点到角两边距离相等
 A
【解析】试题分析:连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
连接NC,MC,在△ONC和△OMC中,
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC
A
【解析】试题分析:连接NC,MC,根据SSS证△ONC≌△OMC,即可推出答案.
连接NC,MC,在△ONC和△OMC中,
∴△ONC≌△OMC(SSS), ∴∠AOC=∠BOC 
