题目内容
13.以下列各组数为三角形的三边,能构成直角三角形的是( )| A. | 4,5,6 | B. | 1,1,$\sqrt{2}$ | C. | 6,8,11 | D. | 5,12,23 |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解答 解:A、42+52≠62,故不是直角三角形,故此选项错误;
B、12+12=($\sqrt{2}$)2,故是直角三角形,故此选项正确;
C、62+82≠112,故不是直角三角形,故此选项错误;
D、52+122≠232,故不是直角三角形,故此选项错误.
故选B.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
3.一只布袋内装有3个红球,6个黑球,1个白球(这些球除颜色外,其余没有区别),从中任意取出一球,则取得的球不是红球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{1}{2}$ |
4.下列各式去括号错误的是( )
| A. | (a-b)-(x-y)=a-b-x+y | B. | m+(-n+a-b)=m-n+a-b | ||
| C. | -2(2x-3y+4)=-4x+6y+4 | D. | x-(3y-1)=x-3y+1 |
1. 如图,菱形ABCD中,已知∠D=110°,则∠BAC=( )
如图,菱形ABCD中,已知∠D=110°,则∠BAC=( )
 如图,菱形ABCD中,已知∠D=110°,则∠BAC=( )
如图,菱形ABCD中,已知∠D=110°,则∠BAC=( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
8.不等式2x-1≤4的最大整数解是( )
| A. | 0 | B. | 1 | C. | $\frac{5}{2}$ | D. | 2 |
5.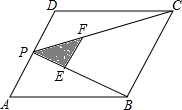 如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
 如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )
如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3,若AD=2,AB=2$\sqrt{3}$,∠A=60°,则S1+S2+S3的值为( )| A. | $\frac{10}{3}$ | B. | $\frac{9}{2}$ | C. | $\frac{13}{3}$ | D. | 4 |
2. 将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )
将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )
 将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )
将一直角三角板与两边平行的纸条如图放置.已知∠2-∠1=30°,则∠2的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
3.在平面直角坐标系中,点(-4,3)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
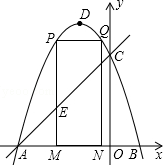 如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.