题目内容
20. 在一次户外拓展训练中,小明攀到一个高为10米的高地A处(如图)看到悬崖顶部O的仰角为30°,利用挂在悬崖顶部的绳索,划过90°到达高为3米的平台B处,求绳索OA的长度和小明在荡绳索的过程中离地面的最低点的高度MN.(小明的身高忽略不计,结果精确到0.01米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次户外拓展训练中,小明攀到一个高为10米的高地A处(如图)看到悬崖顶部O的仰角为30°,利用挂在悬崖顶部的绳索,划过90°到达高为3米的平台B处,求绳索OA的长度和小明在荡绳索的过程中离地面的最低点的高度MN.(小明的身高忽略不计,结果精确到0.01米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 如图,作AP⊥OM、BQ⊥OM,可得AC=PM=10、BD=QM=3、PQ=PM-QM=7,设OA=x,可得OP=$\frac{1}{2}$OA=$\frac{1}{2}$x、AP=OAcos∠OAP=$\frac{\sqrt{3}}{2}$x,证△AOP≌△BOQ得AP=OQ,即$\frac{\sqrt{3}}{2}$x=$\frac{1}{2}$x+7,解之可得x的值;由MN=OP+PM-OQ可得答案.
解答 解:如图,作AP⊥OM于点P、BQ⊥OM于点Q,
则AC=PM=10、BD=QM=3,
∴PQ=PM-QM=7,
设OA=x,
∵∠OAP=30°,
∴OP=$\frac{1}{2}$OA=$\frac{1}{2}$x、AP=OAcos∠OAP=$\frac{\sqrt{3}}{2}$x,
∵∠OAP+∠AOP=90°、∠AOP+∠BOQ=90°,
∴∠OAP=∠BOQ,
在△AOP和△BOQ中,
∵$\left\{\begin{array}{l}{∠APO=∠OQB=90°}\\{∠OAP=∠BOQ}\\{OA=OB}\end{array}\right.$,
∴△AOP≌△BOQ(AAS),
∴AP=OQ,即$\frac{\sqrt{3}}{2}$x=$\frac{1}{2}$x+7,
解得:x=7+7$\sqrt{3}$≈19.12,
即绳索OA的长度约为19.12米;
MN=OP+PM-OQ=$\frac{1}{2}$x+10-$\frac{\sqrt{3}}{2}$x=$\frac{1-\sqrt{3}}{2}$x+10=$\frac{1-\sqrt{3}}{2}$×7(1+$\sqrt{3}$)+10=3.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

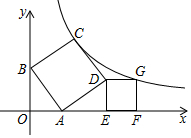 如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )
如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )| A. | 2$+\sqrt{2}$ | B. | 3+$\frac{3}{2}\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 3.6 |
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
 如图所示,左边的正方形与右边的扇形面积相等,扇形的半径和正方形的边长都是2cm,则此扇形的弧长为( )cm.
如图所示,左边的正方形与右边的扇形面积相等,扇形的半径和正方形的边长都是2cm,则此扇形的弧长为( )cm.| A. | 4 | B. | 4π | C. | 8 | D. | 8-π |
 在同一条件下,同一型号的30辆汽车进行耗油1L所行驶的路程的试验,将结果绘制如下频数分布直方图,根据统计图解答下列问题:
在同一条件下,同一型号的30辆汽车进行耗油1L所行驶的路程的试验,将结果绘制如下频数分布直方图,根据统计图解答下列问题: