题目内容
3.直线y=2x+b与x轴、y轴围成的三角形面积为4,则b=±4.分析 先用b表示出直线与x、y轴的交点,再利用三角形的面积公式即可得出结论.
解答 解:解:一次函数y=2x+b与x轴的交点为(-$\frac{b}{2}$,0),与y轴的交点为(0,b).
∵y=2x+b和两坐标轴围成的三角形的面积是4,
∴$\frac{1}{2}$×|-$\frac{b}{2}$|×|b||=4,
∴b=±4.
故答案为:±4.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
11.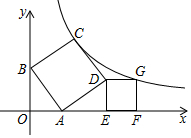 如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )
如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )
 如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )
如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )| A. | 2$+\sqrt{2}$ | B. | 3+$\frac{3}{2}\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 3.6 |
18.已知x2-x-3=0,则x3-4x2+2017的值为( )
| A. | 2008 | B. | 2009 | C. | 2016 | D. | 2017 |
8.已知下列命题:①内错角相等;②无限小数是无理数;③从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;④平行于同一条直线的两条直线平行;⑤两条平行线被第三条直线所截,同旁内角的角平分线互相垂直.其中真命题的个数为( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
15.下列关于变量x.y的关系式:①3x-2y=5:②y=|x+1|;③2x-y2=10.其中表示y是x的函数关系的是( )
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
13. 如图,一圆柱体的底面圆周长为20cm,高AB为4cm,BC是上底的直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,则爬行的最短路程是( )
如图,一圆柱体的底面圆周长为20cm,高AB为4cm,BC是上底的直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,则爬行的最短路程是( )
 如图,一圆柱体的底面圆周长为20cm,高AB为4cm,BC是上底的直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,则爬行的最短路程是( )
如图,一圆柱体的底面圆周长为20cm,高AB为4cm,BC是上底的直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,则爬行的最短路程是( )| A. | 2$\sqrt{29}$ | B. | $\frac{4}{π}$$\sqrt{{π}^{2}+25}$ | C. | 2$\sqrt{25{π}^{2}+4}$ | D. | 14 |
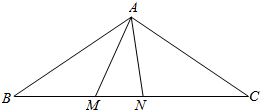 如图,△ABC中,AB=AC,∠B=36°,M,N是BC上两点,且∠AMN=∠ANM=2∠BAM,则图中的等腰三角形一共有( )
如图,△ABC中,AB=AC,∠B=36°,M,N是BC上两点,且∠AMN=∠ANM=2∠BAM,则图中的等腰三角形一共有( ) 在同一条件下,同一型号的30辆汽车进行耗油1L所行驶的路程的试验,将结果绘制如下频数分布直方图,根据统计图解答下列问题:
在同一条件下,同一型号的30辆汽车进行耗油1L所行驶的路程的试验,将结果绘制如下频数分布直方图,根据统计图解答下列问题: