题目内容
2.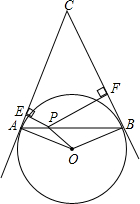 已知:如图所示,P为直径为2的⊙O内一定点,且PO=$\frac{\sqrt{2}}{2}$,线段AB为过点P的任一弦,且它所对的圆心角∠AOB=2θ,再过点A和B作⊙O的切线交于C,设P到AC、BC的距离分别为a、b.求证:a、b是方程2x2-(2ABsinθ)x+sin2θ=0的两个根.
已知:如图所示,P为直径为2的⊙O内一定点,且PO=$\frac{\sqrt{2}}{2}$,线段AB为过点P的任一弦,且它所对的圆心角∠AOB=2θ,再过点A和B作⊙O的切线交于C,设P到AC、BC的距离分别为a、b.求证:a、b是方程2x2-(2ABsinθ)x+sin2θ=0的两个根.
分析 连结CP,OC,OC交AB于H,过点P作直径MN,如图,根据切线长定理和切线的性质得CA=CB,OA⊥CA,OB⊥CB,再判断OC为AB的垂直平分线,得到AH=BH,∠BOH=$\frac{1}{2}$∠AOB=θ,接着利用等角的余角相等得到∠CBA=θ,在Rt△CBH中,根据正弦定义得到CH=BCsinθ,再利用面积法得到$\frac{1}{2}$AC•PE+$\frac{1}{2}$BC•PF=$\frac{1}{2}$CH•AB,整理后得到a+b=ABsinθ;根据正弦定义,在Rt△APE中得到a=APsinθ,在Rt△BPF中得到b=BPsinθ,则ab=AP•BP•sin2θ,然后根据相交弦定理计算出AP•BP=PM•PN=$\frac{1}{2}$,即ab=$\frac{1}{2}$sin2θ,最后利用根与系数的关系写出以a和b为根的一元二次方程即可得到结论.
解答 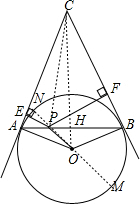 证明:连结CP,OC,OC交AB于H,过点P作直径MN,如图,
证明:连结CP,OC,OC交AB于H,过点P作直径MN,如图,
∵CA和CB为⊙O的切线,
∴CA=CB,OA⊥CA,OB⊥CB,
而OA=OB,
∴OC为AB的垂直平分线,
∴AH=BH,
∴∠BOH=$\frac{1}{2}$∠AOB=θ,
∵∠BOH+∠OBH=90°,∠OBH+∠CBA=90°,
∴∠CBA=θ,
在Rt△CBH中,CH=BCsin∠CBH=BCsinθ,
∵S△CAP+S△CBP=S△CAB,
∴$\frac{1}{2}$AC•PE+$\frac{1}{2}$BC•PF=$\frac{1}{2}$CH•AB,
即a•BC+b•BC=BCsinθ•AB,
∴a+b=ABsinθ;
在Rt△APE中,PE=APsin∠EAP,即a=APsinθ,
在Rt△BPF中,PF=PBsin∠PBF,即b=BPsinθ,
∴ab=AP•BP•sin2θ,
∵AP•BP=PM•PN=(OM+OP)(ON-OP)=(1+$\frac{\sqrt{2}}{2}$)(1-$\frac{\sqrt{2}}{2}$)=1-($\frac{\sqrt{2}}{2}$)2=$\frac{1}{2}$,
∴ab=$\frac{1}{2}$sin2θ,
∴以a和b为根的一元二次方程为x2-ABsinθ+$\frac{1}{2}$sin2θ=0,
即2x2-2ABsinθ+sin2θ=0.
点评 本题考查了圆的综合题:熟练掌握切线的性质、切线长定理和相交弦定理;灵活应用三角形面积公式和锐角三角函数的定义;会运用根与系数的关系写出以两个数为根的一元二次方程.

| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
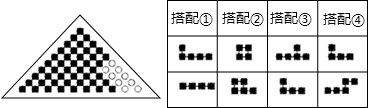
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
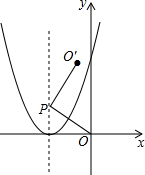 如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1).
如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1). | 度数 | 900 | 920 | 950 | 1010 | 1050 | 1100 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(2)若每度电的定价是0.8元,由上题获得的数据,估计该校每月应付电费是多少?(每月按30天计)
(3)如果做到人走电关,学校每天就可节省电量1%,按照每度电0.8元计算,写出该校节省电费y(元)与天数x(取正整数)之间的函数关系式.

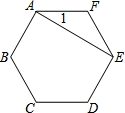 如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$.
如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$.