题目内容
7.在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别分组进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.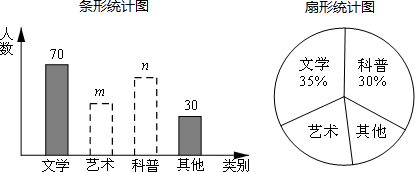
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,样本容量为200,科普类读物这一组的频数是60;
(2)计算扇形统计图总艺术类读物所在扇形的圆心角的度数;
(3)在最喜欢艺术类课外读物的学生组队中,有3名女生,1名男生的美术作品曾获广州市中学生艺术节一等奖,欲从这四人中选出两人担任该组组长(不分正副),用列举法求两人均是女生的概率.
分析 (1)用喜欢文学读物的人数除以喜欢文学读物所占的百分比即可求得样本容量,利用样本容量乘以其所占的百分比即可求得频数;
(2)用喜欢艺术读物的人数所占的百分比乘以周角的度数即可;
(3)根据题意采用列举法,举出所有的可能,注意要做到不重不漏,再根据概率公式即可得出答案.
解答 解:(1)∵观察两个统计图知:喜欢文学读物的有70人,占35%,
∴样本容量为70÷35%=200,
喜欢科普读物的有200×30%=60人;
(3)∵喜欢艺术的有200-30-70-60=40,
∴艺术类读物所在扇形的圆心角的度数为$\frac{40}{200}$×360°=72°;
(3)用A1,A2,A3表示3名女生,B表示1名男生,
则从4人中选出2人的情况有:(A1,A2),(A1,A3),(A1,B),(A2,A3),(A2,B),(A3,B),共计6种,
选出的2人均是女生(A1,A2),(A1,A3),(A2,A3)共计3种,
则两人均是女生的概率$\frac{3}{6}$=$\frac{1}{2}$.
点评 此题考查了扇形图与概率的知识,综合性比较强,解题时要注意认真审题,理解题意;在用列举法求概率时,一定要注意不重不漏.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
18.某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x套服装,则根据题意可得方程为( )
| A. | $\frac{160}{x}$+$\frac{400-160}{(1+20%)x}$=18 | B. | $\frac{160}{x}$+$\frac{400}{(1+20%)x}$=18 | ||
| C. | $\frac{160}{x}$+$\frac{400-160}{20%x}$=18 | D. | $\frac{400}{x}$+$\frac{400-160}{(1+20%)x}$=18 |
12.-2的相反数的倒数是( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
19.若$\frac{{\sqrt{x-3}}}{x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥3 | B. | x≤3且x≠1 | C. | 1<x≤3 | D. | x≥1且x≠3 |

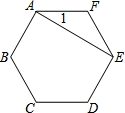 如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$.
如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$.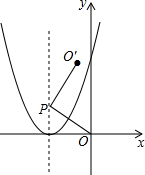 如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1).
如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1).