题目内容
3.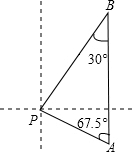 在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73)
在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73)
分析 首先根据题意可得PC⊥AB,然后设PC=x海里,分别在Rt△APC中与Rt△PCB中,利用正切函数求得出AC与BC的长,由AB=21×5,即可得方程,解此方程即可求得x的值,继而求得答案.
解答 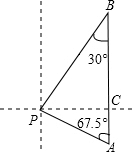 解:过点P作PC⊥AB,垂足为C,设PC=x海里.
解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=$\frac{PC}{AC}$,
∴AC=$\frac{PC}{tan67.5°}$=$\frac{5x}{12}$.
在Rt△PCB中,∵tan∠B=$\frac{PC}{BC}$,
∴BC=$\frac{x}{tan30°}$=$\sqrt{3}$x,PB=2PC=2x.
∵AC+BC=AB=21×5,
∴$\frac{5x}{12}$+$\sqrt{3}$x=105,
解得x≈48.86,
∴PB=2x≈97.7(海里).
答:此时轮船所处位置B与小岛P的距离约为97.7海里.
点评 此题考查了方向角问题.此题难度适中,注意结合实际问题,利用解直角三角形的相关知识求解是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
8.若a、b是有理数,且|a|=1,|b|=2,ab<0,则a+b=( )
| A. | 1或-3 | B. | 3或-1 | C. | 3或-3 | D. | 1或-1 |
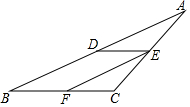 如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?
如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?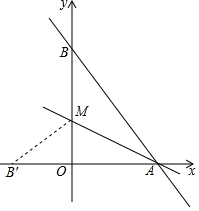 直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).
直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).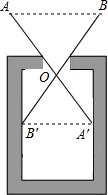 如图,将两根等长钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工作,则AB的长等于容器内径A′B′,那么判定△OAB≌△OA′B′的理由是SAS.
如图,将两根等长钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成了一个测量工作,则AB的长等于容器内径A′B′,那么判定△OAB≌△OA′B′的理由是SAS.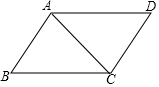 如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由.
如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由.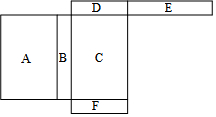 如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题.
如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题. 如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6).
如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6).