题目内容
15.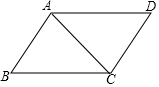 如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由.
如图,在四边形ABCD中,已知AB∥CD,∠B=∠D,在说明∠DAC=∠BCA的解答过程中,填上适当的理由.解:∵AB∥CD(已知)
∴∠BAC=∠DCA(两直线平行,内错角相等)
∠B+∠BCD=180°
∠D+∠BAD=180°(两直线平行,同旁内角互补)
∵∠B=∠D(已知)
∴∠BCD=∠BAD(补角的性质)
∵∠DAC=∠BAD-∠BAC
∠BCA=∠BCD-∠DCA(已知)
∴∠DAC=∠BCA(等量代换)
分析 根据平行线的性质即可得到结论.
解答 解:∵AB∥CD(已知)
∴∠BAC=∠DCA(两直线平行,内错角相等)
∠B+∠BCD=180°
∠D+∠BAD=180°(两直线平行,同旁内角互补)
∵∠B=∠D(已知)
∴∠BCD=∠BAD(补角的性质)
∵∠DAC=∠BAD-∠BAC
∠BCA=∠BCD-∠DCA(已知)
∴∠DAC=∠BCA(等量代换).
故答案为:两直线平行,内错角相等,补角的性质,等量代换.
点评 本题考查了平行线的性质,熟练掌握平行线的性质定理是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
5.-|-2|的结果为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
 如图,AB∥CD,直线EF分别交AB、CD于点E、F,CE平分∠AEF,DE⊥CE,若∠ECF=42°,则∠FED=48°.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,CE平分∠AEF,DE⊥CE,若∠ECF=42°,则∠FED=48°.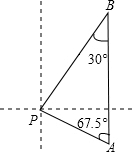 在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73)
在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73) 如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数至少4个.
如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数至少4个.