题目内容
14．若关于x的一元二次方程x2-2x+$\frac{k}{2}$=0没有实根，那么k的最小正整数值是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 首先根据一元二次方程x2-2x+$\frac{k}{2}$=0没有实根得到△=（-2）2-4×$\frac{k}{2}$＜0，进而求出k的取值范围，最后得出k的最小正整数值．
解答 解：∵一元二次方程x2-2x+$\frac{k}{2}$=0没有实根，
∴△=（-2）2-4×$\frac{k}{2}$＜0，
∴k＞2，
∴k的最小正整数值是3，
故选C．
点评 本题主要考查了根的判别式的知识，解答本题要掌握一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根．
练习册系列答案
全能测控一本好卷系列答案
相关题目
4．
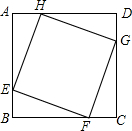如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（ ）
如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（ ）| A． | 30 | B． | 34 | C． | 36 | D． | 40 |
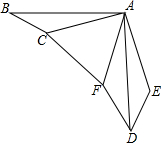如图，在△ABC中，∠BAC=15°，将△ABC绕点A按逆时针方向旋转90°，到△ADE的位置，然后将△ADE以AD为轴翻折到△ADF的位置，连接CF，判断△ACF的形状，并说明理由．
如图，水平放置的长方体的底面是边长为2cm和4cm的矩形，它的左视图的面积为6cm2，则长方体的体积是多少？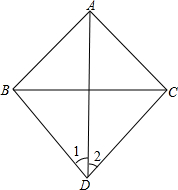
已知△ABC是等腰直角三角形，∠BAC=90°，在△ABC所在平面内有点D（点D不在△ABC内部也不在其边上），如图，连接BD、AD、CD，若∠1=∠2，求证：∠DBC=∠DCB．
6．如果把$\frac{2y}{2x-3y}$中的x和y都扩大10倍，那么分式的值（ ）
| A． | 不变 | B． | 扩大10倍 | C． | 缩小10倍 | D． | 扩大20倍 |