题目内容
 如图,在?ABCD中,AE⊥BC于点E,AF⊥DC于F,∠EAF=60°,BE=
如图,在?ABCD中,AE⊥BC于点E,AF⊥DC于F,∠EAF=60°,BE=| 3 |
考点:平行四边形的性质
专题:
分析:由在?ABCD中,AE⊥BC于点E,AF⊥DC于F,∠EAF=60°,即可求得∠C=120°,继而求得∠B=∠C=60°,又由BE=
cm,FD=3cm,即可求得AB与AD的长,继而求得答案.
| 3 |
解答:解:∵AE⊥BC,AF⊥DC,∠EAF=60°,
∴∠C=360°-∠AEC-∠C-∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠B=∠C=60°,
∴∠BAE=∠DAF=30°,
∵BE=
cm,FD=3cm,
∴AB=2BE=2
(cm),AD=2FD=6(cm),
∴?ABCD的周长为:2(AB+AD)=4
+12(cm).
∴∠C=360°-∠AEC-∠C-∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠B=∠C=60°,
∴∠BAE=∠DAF=30°,
∵BE=
| 3 |
∴AB=2BE=2
| 3 |
∴?ABCD的周长为:2(AB+AD)=4
| 3 |
点评:此题考查了平行四边形的性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
下面计算正确的是( )
| A、b3b2=b6 |
| B、x3+x3=x6 |
| C、a4+a2=a6 |
| D、mm5=m6 |
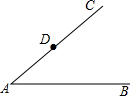 如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)
如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)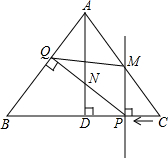 已知,如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于D,直线PM从点C出发沿CB方向匀速运动,速度为1cm/s;运动过程中始终保持PM⊥BC,直线PM交BC于P,交AC于点M;过点P作PQ⊥AB,交AB于Q,交AD于点N,连接QM,设运动时间是t(s)(0<t<6),解答下列问题:
已知,如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于D,直线PM从点C出发沿CB方向匀速运动,速度为1cm/s;运动过程中始终保持PM⊥BC,直线PM交BC于P,交AC于点M;过点P作PQ⊥AB,交AB于Q,交AD于点N,连接QM,设运动时间是t(s)(0<t<6),解答下列问题: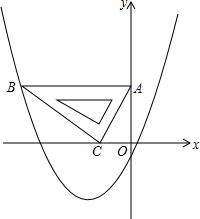 在平面直角坐标系中,现将一块含30°的直角三角板ABC放在第二象限,30°角所对的直角边AC斜靠在两坐标轴上,且点A(0,3),点C(-
在平面直角坐标系中,现将一块含30°的直角三角板ABC放在第二象限,30°角所对的直角边AC斜靠在两坐标轴上,且点A(0,3),点C(-