题目内容
12．在直角坐标系中，已知点A（0，4）、B（4，4）和C（6，2）．（1）点A、B、C能确定一个圆吗？说明理由；
（2）如果能，用尺规作图的方法，作出过这三点的圆的轨迹；
（3）写出圆心P的坐标，并求出⊙P的半径．
分析 （1）根据不在同一条直线上的三个点确定一个圆，可得答案；
（2）根据线段垂直平分线的性质，可得圆心，可得圆；
（3）根据线段垂直平分线的性质，可得圆心，根据勾股定理，可得半径．
解答 解：（1）点A、B、C能确定一个圆，理由是：点A、B、C不在同一条直线上；
（2）如图：
；
（3）由AB的垂直平分线，BC的垂直平分线的交点，得
圆心的坐标是（2，0），
半径的长为$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$．
点评 本题考查了确定圆的条件，不在同一条直线上的三点确定一个圆，线段垂直平分线的交点是圆心．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
5．
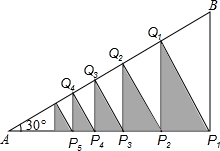如图，在Rt△ABP1中，∠AP1B=Rt∠，∠A=30°，BP1=2，过点P1作P1Q1⊥AB，垂足Q1，过点Q1作Q1P2⊥AP1，垂足P2，过点P2作P2Q2⊥AB，垂足Q2，…如此无限下去，得到一系列阴影三角形△P1Q1P2、△P2Q2P3、△P3Q3P4…，则所有这些阴影三角形的面积和是（ ）
如图，在Rt△ABP1中，∠AP1B=Rt∠，∠A=30°，BP1=2，过点P1作P1Q1⊥AB，垂足Q1，过点Q1作Q1P2⊥AP1，垂足P2，过点P2作P2Q2⊥AB，垂足Q2，…如此无限下去，得到一系列阴影三角形△P1Q1P2、△P2Q2P3、△P3Q3P4…，则所有这些阴影三角形的面积和是（ ）| A． | $\sqrt{3}$ | B． | $\frac{3}{4}\sqrt{3}$ | C． | $\frac{6}{7}\sqrt{3}$ | D． | 不能确定 |
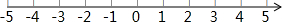已知在纸面上有一数轴（如图），折叠纸面．
已知：如图，CD⊥AB于D，BE⊥AC于E，∠1=∠2．求证：OB=OC．