题目内容
3. 已知:如图,CD⊥AB于D,BE⊥AC于E,∠1=∠2.求证:OB=OC.
已知:如图,CD⊥AB于D,BE⊥AC于E,∠1=∠2.求证:OB=OC.
分析 根据全等三角形的判定与性质,可得OD与OE的关系,根据ASA,可得△OBD与△OCE的关系,根据全等三角形的性质,可得答案.
解答 证明:∵CD⊥AB于D,BE⊥AC于E,
∴∠ODA=∠OEA=90°.
在△ODA和△OEA中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠ODA=∠OEA}\\{AO=AO}\end{array}\right.$,
∴△ODA≌△OEA (AAS),
∴OD=OE.
在△OBD和△OCE中,
$\left\{\begin{array}{l}{∠ODB=∠OEC=90°}\\{OD=OE}\\{∠BOD=∠COE(对顶角相等)}\end{array}\right.$,
∴△OBD≌△OCE (ASA),
∴OB=OC.
点评 本题考查了全等三角形的判定与性质,利用公共边OA是证明△ODA≌△OEA的关键,又利用对顶角的性质得出∠BOD=∠COE,利用已知条件选择恰当的判定方法是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.一次函数的一般形式是(k、b是常数)( )
| A. | y=kx+b | B. | y=kx | C. | y=kx+b(k≠0) | D. | y=x |
11.若抛物线y=a(x-2)2+a2+a顶点在x轴上,则a的值为( )
| A. | -1 | B. | 0 | C. | 0或-1 | D. | 任意实数 |
13.南昌市某路公交车共有10站,我们把上客人数记为“+”,把下客人数记为“-”,一次该路一辆公交车各站上、下人数列表如下:
(1)求表格中x的值;
(2)求在⑤、⑥站之间该公交车上的人数;
(3)问在哪两站之间,该公交车上的人数最多?并求最多人数.
| ①始发站 | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩终点站 | |
| 上客人数 | 9 | 8 | 10 | 12 | 14 | 13 | 11 | 6 | 7 | 0 |
| 下客人数 | 0 | -3 | -5 | -7 | -4 | -8 | -6 | -9 | x | -28 |
(2)求在⑤、⑥站之间该公交车上的人数;
(3)问在哪两站之间,该公交车上的人数最多?并求最多人数.
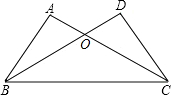 如图,AC与BD交于O点,若AB=DC,请补充一个条件:AC=BD(或∠ABC=∠DCB等),使△ABC≌△DCB.
如图,AC与BD交于O点,若AB=DC,请补充一个条件:AC=BD(或∠ABC=∠DCB等),使△ABC≌△DCB.