题目内容
19.已知4<a<11,化简:$\sqrt{{{(a-4)}^2}}+\sqrt{{{(a-11)}^2}}$.分析 首先确定出a-4、a-11的正负情况,然后依据$\sqrt{{a}^{2}}$=|a|进行化简,最后化简绝对值、合并同类项即可.
解答 解:∵4<a<11,
∴a-4>0,a-11<0.
∴$\sqrt{{{(a-4)}^2}}+\sqrt{{{(a-11)}^2}}$=|a-4)|+|a-11|=a-4+11-a=7.
点评 本题主要考查的是二次根式的性质与化简,依据$\sqrt{{a}^{2}}$=|a|进行化简是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列实数中,无理数是( )
| A. | $\sqrt{16}$ | B. | 3.14159 | C. | 0 | D. | -$\sqrt{12}$ |
14.函数$y=\sqrt{\frac{1}{2x-1}}$中,自变量x的取值范围是( )
| A. | $x>\frac{1}{2}$ | B. | $x≥\frac{1}{2}$ | C. | $x<\frac{1}{2}$ | D. | $x≠\frac{1}{2}$ |
4. 如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
 如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{AE}{EC}=\frac{BF}{FC}$ | B. | $\frac{AD}{BF}=\frac{AB}{BC}$ | C. | $\frac{EF}{AB}=\frac{DE}{BC}$ | D. | $\frac{CE}{CF}=\frac{EA}{BF}$ |
11.已知a>0,b<0,|a|<|b|,则( )
| A. | a+b<0 | B. | b-a>0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
 如图是钢琴键盘的一部分,若从4开始,依次弹出4,5,6,7,1,4,5,6,7,1,…,按照上述规律弹到第2016个音符是4.
如图是钢琴键盘的一部分,若从4开始,依次弹出4,5,6,7,1,4,5,6,7,1,…,按照上述规律弹到第2016个音符是4.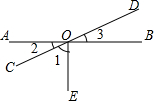 如图,已知直线AB、CD交于点O,OE⊥AB于O,∠1=65°,求∠3的度数.
如图,已知直线AB、CD交于点O,OE⊥AB于O,∠1=65°,求∠3的度数.