题目内容
4. 如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{AE}{EC}=\frac{BF}{FC}$ | B. | $\frac{AD}{BF}=\frac{AB}{BC}$ | C. | $\frac{EF}{AB}=\frac{DE}{BC}$ | D. | $\frac{CE}{CF}=\frac{EA}{BF}$ |
分析 根据平行线分线段成比例定理列出比例式,再分别对每一项进行判断即可.
解答 A.∵EF∥AB,∴$\frac{AE}{EC}$=$\frac{BF}{FC}$,故本选项正确,
B.∵DE∥BC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,
∵EF∥AB,
∴DE=BF,
∴$\frac{AD}{AB}$=$\frac{BF}{BC}$,
∴$\frac{AD}{BF}$=$\frac{AB}{BC}$,
故本选项正确,
C.∵EF∥AB,
∴$\frac{EF}{AB}$=$\frac{CF}{BC}$,
∵CF≠DE,
∴$\frac{EF}{AB}$≠$\frac{DE}{BC}$,
故本选项错误,
D.∵EF∥AB,
∴$\frac{CE}{EA}$=$\frac{CF}{BF}$,
∴$\frac{CE}{CF}$=$\frac{EA}{BF}$,
故本选项正确,
故选:C.
点评 此题主要考查平行线分线段成比例定理,关键是根据平行线分线段成比例定理列出比例式并能进行灵活变形.

练习册系列答案
相关题目
15.已知直角三角形的一个锐角为60°,斜边长为1,那么此直角三角形的面积是( )
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
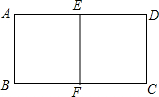 用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2.
用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2. 如图,a∥b,c∥d,若∠1=68°,求∠2、∠3的度数.
如图,a∥b,c∥d,若∠1=68°,求∠2、∠3的度数.