题目内容
9.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S随矩形一边长x(单位:米)的变化而变化.(1)求S与x之间的函数关系式.
(2)当x是多少时,矩形场地的面积S最大;最大面积是多少?
分析 (1)已知周长为60米,一边长为x,则另一边长为30-x.
(2)用配方法化简函数解析式,求出s的最大值.
解答 解:(1)根据题意,矩形另一边长为:$\frac{60-2x}{2}$=30-x米,
故S=x(30-x);
(2)∵S=x(30-x)
=-(x-15)2+225,
∴当x=15时,S有最大值为225平方米.
即当x是15时,矩形场地面积S最大,最大面积是225平方米.
点评 本题考查的是二次函数的应用,根据题意表示出另一边长是根本,将长乘以宽得出面积并配方找最大值是关键.

练习册系列答案
相关题目
20.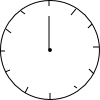 如图,一个挂钟分针长10cm,经过40分钟,它的针尖转过的弧长是( )
如图,一个挂钟分针长10cm,经过40分钟,它的针尖转过的弧长是( )
 如图,一个挂钟分针长10cm,经过40分钟,它的针尖转过的弧长是( )
如图,一个挂钟分针长10cm,经过40分钟,它的针尖转过的弧长是( )| A. | 40πcm | B. | $\frac{40}{3}$πcm | C. | $\frac{20}{3}$πcm | D. | $\frac{100}{9}$πcm |
17.直径小于或等于2.5微米的颗粒物又称作PM2.5,也称为细颗粒物或可入肺颗粒物,相当于头发丝直径的$\frac{1}{20}$,可直接进入肺部,以室内PM2.5为85微克/立方米,轻度污染指数为130(轻度污染)计算,则每天吸入鼻孔,咽喉,肺及血液里的有毒颗粒物和有害气体总数约为850毫克,若1千克=1000000毫克,则850毫克用科学记数法可记作( )
| A. | 850×106千克 | B. | 8.50×10-4千克 | C. | 0.850×10-4千克 | D. | 850×10-4千克 |
1.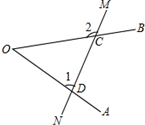 如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )
如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )
 如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )
如图,直线MN和∠AOB的两边分别相交于点C,D.已知∠O=40°,∠2=125°,则∠1=( )| A. | 85° | B. | 75° | C. | 65° | D. | 55° |
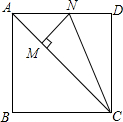 如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.
如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.