题目内容
 如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F.
如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F.(1)求证:AEPF是矩形;
(2)D为BC中点,连接DE,DF.求证:DE=DF.
考点:矩形的判定,全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)首先利用平行线的定义判定平行四边形,然后利用有一个角是直角的平行四边形是矩形判定矩形;
(2)再根据矩形的性质可得出AE=FP,由Rt△ABC中,∠BAC=90°,AB=AC,D为BC中点可得出AD=BC再由全等三角形的判定定理可得出△ADE≌△CDF,进而可得出结论.
(2)再根据矩形的性质可得出AE=FP,由Rt△ABC中,∠BAC=90°,AB=AC,D为BC中点可得出AD=BC再由全等三角形的判定定理可得出△ADE≌△CDF,进而可得出结论.
解答:证明:(1)∵∠BAC=90°,PE⊥AB,
∴PE∥AF,
∴PF∥AE,
∴AEPF是平行四边形,
∵PE⊥AB,
∴AEPF是矩形;
(2)连接DA,
∵∠BAC=90°,AB=AC,D为BC中点,
∴DA=DC,∠DAE=∠DCF=135°,
又由(1)知AE=PF,△CFP是等腰直角三角形,
∴CF=PF=AE,
∴△DAE≌△DCF,
∴DE=DF
∴PE∥AF,
∴PF∥AE,
∴AEPF是平行四边形,
∵PE⊥AB,
∴AEPF是矩形;
(2)连接DA,
∵∠BAC=90°,AB=AC,D为BC中点,
∴DA=DC,∠DAE=∠DCF=135°,
又由(1)知AE=PF,△CFP是等腰直角三角形,
∴CF=PF=AE,
∴△DAE≌△DCF,
∴DE=DF
点评:本题考查的是矩形的判定与性质、全等三角形的判定与性质、三角形内角和定理,涉及面较广,难度适中.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
在Rt△ABC中,∠C为直角,AC=6,BC=8,则sinA=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB为( )
如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB为( )| A、10cm | B、16cm |
| C、8cm | D、12cm |
 如图,数轴上点A示数a,点B表示数b,则下列结论正确的是( )
如图,数轴上点A示数a,点B表示数b,则下列结论正确的是( )| A、ab<0 |
| B、|a|<|b| |
| C、b-a<0 |
| D、b-a>0 |
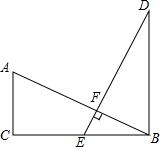 如图,已知AC⊥CB,DB⊥CB,AB⊥DE,AB=DE,E是BC的中点.
如图,已知AC⊥CB,DB⊥CB,AB⊥DE,AB=DE,E是BC的中点. 如图,已知过坐标轴上A、C两点的直线y=x+3和过这两点的抛物线y=-x2+bx+c,抛物线与x轴的另一交点为B,求抛物线解析式.
如图,已知过坐标轴上A、C两点的直线y=x+3和过这两点的抛物线y=-x2+bx+c,抛物线与x轴的另一交点为B,求抛物线解析式. 如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.  已知一次函数y=kx+b的图象平行于直线y=-2x+4,且经过点A(2,-2).
已知一次函数y=kx+b的图象平行于直线y=-2x+4,且经过点A(2,-2).