Question

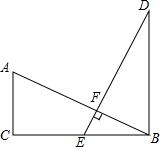如图，已知AC⊥CB，DB⊥CB，AB⊥DE，AB=DE，E是BC的中点．
（1）观察并猜想BD和BC有何数量关系？并证明你猜想的结论．
（2）若BD=6cm，求AC的长．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）BD=BC，可通过证明△ABC与△EDB全等得到；
（2）由（1）中的结论可得BD=BC，AC=BE=

1

2

BD=3cm．

解答：解：（1）BD和BC相等．
理由如下：
∵AC⊥CB，DB⊥CB，
∴∠ACB=∠DBE=90°，
∵AB⊥DE，
∴∠DEB+∠FBE=90°，
∵∠D+∠DEB=90°，
∴∠D=∠ABC，
在ABC与△EDB中，

∠C=∠DBE ∠ABC=∠D AB=DE

，
∴△ABC≌△EDB（AAS）；
（2）∵△ABC≌△EDB，
∴BC=BD=6cm，AC=BE，
∵E是BC的中点，
∴BE=CE=

1

2

BC=3cm，
∴AC=BE=3cm．

点评：本题考查了垂直的定义、全等三角形的判定和性质、中点的定义以及互余两角的性质，属于中考常见题型，比较简单．