题目内容
13.某商场用18万元购进A、B两种商品,其进价和售价如下表:| A | B | |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1380 | 1200 |
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
分析 (1)由题意可知本题的等量关系,即“两种商品总成本为18万元”和“共获利3万元”,根据这两个等量关系,可列出方程组,再求解;
(2)根据题意列出不等式组,解答即可.
解答 解:(1)设购进A种商品x件,B种商品y件.
根据题意得$\left\{\begin{array}{l}{1200x+1000y=180000}\\{(1380-1200)x+(1200-1000)y=30000}\end{array}\right.$
化简得$\left\{\begin{array}{l}{6x+5y=900}\\{9x+10y=1500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=100}\\{y=60}\end{array}\right.$,
答:该商场购进A种商品100件,B种商品60件;
(2)设购进A种商品x件,B种商品y件.
根据题意得:$\left\{\begin{array}{l}{1200x+1000y=180000}\\{y≥6x}\\{y>0}\\{y<180}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=25}\\{y=150}\end{array}\right.$,$\left\{\begin{array}{l}{x=20}\\{y=156}\end{array}\right.$,$\left\{\begin{array}{l}{x=15}\\{y=162}\end{array}\right.$,$\left\{\begin{array}{l}{x=10}\\{y=168}\end{array}\right.$,$\left\{\begin{array}{l}{x=5}\\{y=174}\end{array}\right.$,
故共有5种进货方案
| A | B | |
| 方案一 | 25件 | 150件 |
| 方案二 | 20件 | 156件 |
| 方案三 | 15件 | 162件 |
| 方案四 | 10件 | 168件 |
| 方案五 | 5件 | 174件 |
点评 此题考查二元一次方程组和一元一次不等式的应用,解答本题的关键是将现实生活中的事件与数学思想联系起来,读懂题意,找出等量关系,列方程求解.

| A. | 6,6 | B. | 6,8 | C. | 7,6 | D. | 7,8 |
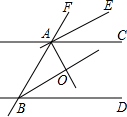 如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证:
如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证: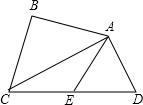 如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=1,AC=$\sqrt{2}$,点E为CD中点.求证:CD=2AE.
如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=1,AC=$\sqrt{2}$,点E为CD中点.求证:CD=2AE.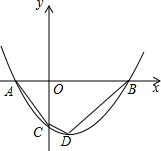 如图所示,在平面直角坐标系中,抛物线经过点A(-1,0),B(3,0),C(0,-1)三点.
如图所示,在平面直角坐标系中,抛物线经过点A(-1,0),B(3,0),C(0,-1)三点.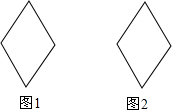 如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.
如图1、2是两个全等的菱形,边长为2cm,最小内角为60°.