题目内容
11.-2xm+2y4与3x3yn-1互为同类项,请求出2m+n的值.分析 利用同类项所含字母相同,并且相同字母的指数也相同求解即可.
解答 解:∵-2xm+2y4与3x3yn-1互为同类项,
∴有m+2=3,n-1=4,
∴m=1,n=5,
∴2m+n=2×1+5=7.
点评 本题主要考查了同类项,解题的关键是熟记同类项的定义.

练习册系列答案
相关题目
1.一个n边形的内角和比它的外角和至少大120°,则n的最小值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
16.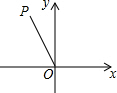 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )
 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )| A. | (2,4) | B. | (-2,4) | C. | (-2,2$\sqrt{3}$) | D. | (-2$\sqrt{3}$,2) |
1.某班体育委员记录第一组七位同学定点投篮(每人投十个),投进篮筐的个数情况依次是:5,6,5,3,6,8,9.则这组数据的平均数和中位数分别是( )
| A. | 6,6 | B. | 6,8 | C. | 7,6 | D. | 7,8 |
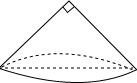 如图,圆锥的主视图是一个等腰直角三角形,直角边长为2,则这个圆锥的侧面积为2$\sqrt{2}$π.(结果保留π)
如图,圆锥的主视图是一个等腰直角三角形,直角边长为2,则这个圆锥的侧面积为2$\sqrt{2}$π.(结果保留π)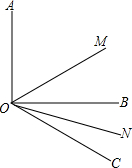 (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;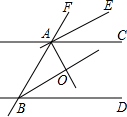 如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证:
如图,直线AC∥BD,AE、AO、BO分别是∠CAF、∠BAC、∠ABD的平分线.求证: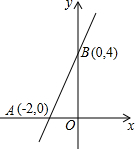 如图,一次函数y=kx+b(k≠0)与坐标轴交于点A,B,则△AOB的面积为4.
如图,一次函数y=kx+b(k≠0)与坐标轴交于点A,B,则△AOB的面积为4.