题目内容
4.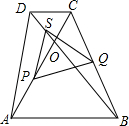 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.(1)求证:△SPQ是等边三角形;
(2)若AB=5,CD=3,求△SPQ的面积.
分析 (1)连接SC、PB,根据等腰三角形性质、直角三角形斜边中线、三角形中位线可判断出答案;
(2)根据等腰梯形的性质及∠ABD=60°可求出等边三角形的边长,从而可得出答案.
解答 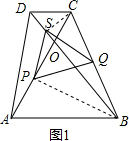 解:(1)连接SC、PB,
解:(1)连接SC、PB,
∵四边形ABCD为等腰梯形,
∴AD=BC,∠ADC=∠BCD,
又∵DC=CD,
∴△ADC≌△BCD,
∴∠ODC=∠OCD,
∴OD=OC,即△ODC是等腰三角形,
∵∠ACD=60°,
∴△ODC是等边三角形,
∵S为OD的中点,
∴CS⊥DO,同理BP⊥AP,
又∵Q为BC的中点,即SQ为Rt△BSC斜边上的中线,
∴PS=$\frac{1}{2}$AD,SQ=$\frac{1}{2}$BC,PQ=$\frac{1}{2}$BC,
∴△SPQ是等边三角形;
(2)如图2,作DE⊥AB,垂足为E,
∵AB=5,CD=3,
∴AE=$\frac{5-3}{2}$=1,BE=5-1=4,
∵由①得,△OCD是等边三角形,
∴△OAB是等边三角形,
∴∠ABD=60°,
∴DE=BE•tan60°=4$\sqrt{3}$.
在Rt△ADE中,
∵AD=$\sqrt{{AE}^{2}+{DE}^{2}}$=$\sqrt{{1}^{2}+{(4\sqrt{3})}^{2}}$=7,
∴PS=PQ=SQ=$\frac{7}{2}$,
∴S△PQS=$\frac{49\sqrt{3}}{16}$.
点评 本题考查等腰梯形及等边三角形的知识,解答此题的关键是作出辅助线,构造出直角三角形,利用直角三角形的性质求解.

练习册系列答案
相关题目
15.抛物线y=-$\frac{1}{2}$(x-2)2+1的顶点坐标是( )
| A. | (-2,-1) | B. | (-2,1) | C. | (2,-1) | D. | (2,1) |
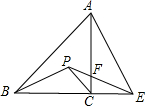 如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.
如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.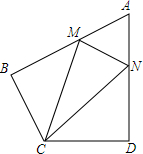 如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,MC=NC,求证:△AMN是等边三角形.
如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,MC=NC,求证:△AMN是等边三角形.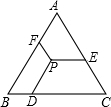 如图所示,△ABC是等边三角形,P是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=8.
如图所示,△ABC是等边三角形,P是其内任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=8.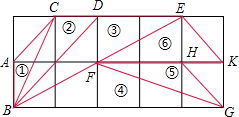 如图,在正方形网格上有6个斜三角形:
如图,在正方形网格上有6个斜三角形: