题目内容
19.解方程组:$\left\{\begin{array}{l}{3x-y+z=10①}\\{x+2y-z=6②}\\{x+y+2z=17③}\end{array}\right.$.分析 ①+②消去z得到一个方程,记作④,②×2+③消去z得到另一个方程,记作⑤,两方程联立消去y求出x的值,将x的值代入④求出y的值,将x、y的值代入③求出z的值,即可得到原方程组的解.
解答 解:①+②得:4x+y=16④,
②×2+③得:3x+5y=29⑤,
④⑤组成方程组$\left\{\begin{array}{l}{4x+y=16}\\{3x+5y=29}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$
将x=3,y=4代入③得:z=5,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=4}\\{z=5}\end{array}\right.$.
点评 此题考查了三元一次方程组的解法,利用了消元的思想,消元的方法有两种:加减消元法;代入消元法,熟练掌握两种方法是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.下列多项式因式分解错误的是( )
| A. | am+bm=(a+b)m | B. | a2-b2=(a+b)(a-b) | ||
| C. | a2-2ab+b2=(a-b)2 | D. | 4x2+4y2+8xy=(2x+2y)2 |
11.已知x2+y2+4x-6y+13=0,则代数式x+y的值为( )
| A. | -1 | B. | 1 | C. | 25 | D. | 36 |
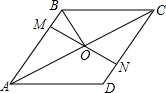 如图,在?ABCD中,对角线AC平分∠BAD,MN与AC交于点O,M,N分别在AB,CD上,且AM=CN,连接BO.若∠DAC=28°,则∠OBC的度数为62°.
如图,在?ABCD中,对角线AC平分∠BAD,MN与AC交于点O,M,N分别在AB,CD上,且AM=CN,连接BO.若∠DAC=28°,则∠OBC的度数为62°. 甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )
甲、乙两人在一段长1200米的直线公路上进行跑步练习,起跑时乙在起点,甲在乙前面,若甲乙同时起跑至乙到达终点的过程中,甲乙之间的距离y(米)与时间t(秒)之间的函数关系如图所示,有下列说法:①甲的速度为4米/秒;②50秒时乙追上甲;③经过25秒时甲乙相距50米;④乙到达终点时甲距终点40米.其中正确的说法有( )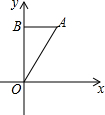 如图:在平面直角坐标系中,点A的坐标(2,4),点B的坐标(0,4),将△AOB绕点O旋转90°至△COD位置(其中点C与点A是对应点,点D与点B是对应点),OD落在x轴上,则点C的坐标是(4,-2),(-4,2).
如图:在平面直角坐标系中,点A的坐标(2,4),点B的坐标(0,4),将△AOB绕点O旋转90°至△COD位置(其中点C与点A是对应点,点D与点B是对应点),OD落在x轴上,则点C的坐标是(4,-2),(-4,2).