题目内容
13.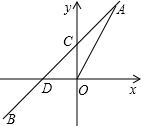 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.(1)m=1;
(2)若一次函数图象经过点B(-2,-1),求一次函数的解析式;
(3)在(2)的条件下,求△AOD的面积.
分析 (1)根据正比例函数解析式求得m的值,
(2)进一步运用待定系数法求得一次函数的解析式;
(3)根据(2)中的解析式,令y=0求得点D的坐标,从而求得三角形的面积.
解答 解:(1)∵正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),
∴2m=2,
m=1.
故答案为:1;
(2)把(1,2)和(-2,-1)代入y=kx+b,得
$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=-1}\end{array}\right.$,
解,得
$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
则一次函数解析式是y=x+1;
(3)令y=0,则x=-1.
则△AOD的面积=$\frac{1}{2}$×1×2=1.
点评 此题综合考查了待定系数法求函数解析式、直线与坐标轴的交点的求法,关键是根据正比例函数解析式求得m的值.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
3.∠AOB是平角,从点O引射线OC,使∠AOC:∠BOC=1:5,OD是∠BOC的角平分线,则∠COD的度数是( )
| A. | 50° | B. | 65° | C. | 70° | D. | 75° |
4.某商店购进一种商品,单价为30元试销中发现这种商品每天的销售量P(件)与每件的销售价x(元)满足P=100-3x.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( )
| A. | (x-30)(100-3x)=200 | B. | x(100-3x)=200 | C. | (30-x)(100-3x)=200 | D. | (x-30)(3x-100)=200 |
18.二次函数y=x2+x的图象与y轴的交点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | (0,0) | D. | (-1,0) |
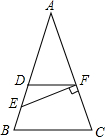 如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.
如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.