题目内容
3.在一个不透明的布袋中有1个红球,1个绿球和2个白球,这些球除颜色外无其他差别.(1)从袋中随机摸出一个球,摸到绿球和摸到白球的可能性不相同(填“相同”或“不相同”);
(2)从袋中随机摸出一个球,不放回,再随机摸出一个球,用列表法或画树状图法求从袋中两次摸出不同颜色球的概率.
分析 (1)先利用概率公式分别计算出摸到绿球和摸到白球的概率,然后根据概率的大小判断可能性是否相同;
(2)先画树状图展示12种等可能的结果数,再找出两次摸出不同颜色球的结果数,然后根据概率公式求解.
解答 解:(1)摸到绿球的概率=$\frac{1}{4}$,摸到白球的概率=$\frac{2}{4}$=$\frac{1}{2}$,
所以摸到绿球和摸到白球的可能性不相同;
故答案为不相同;
(2)画树状图为:
共有12种等可能的结果数,其中两次摸出不同颜色球的结果数2,
所以两次摸出不同颜色球的概率=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知等边△ABC的一边长为10,则它的周长是( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
11.已知圆的半径为4,一点到圆心的距离是5,则这点在( )
| A. | 圆内 | B. | 圆上 | C. | 圆外 | D. | 都有可能 |
8.解方程$\frac{x+1}{2}$-$\frac{x-3}{6}$=1时,下列去分母正确的是( )
| A. | 3x+1-x-3=1 | B. | 3(x+1)-(x-3)=1 | C. | 3(x+1)-x-3=6 | D. | 3(x+1)-(x-3)=6 |
15.十八世纪瑞士数学家欧拉证明了简单多面体的顶点数(V)、面树(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
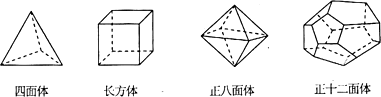
(1)根据上面多面体模型,填写表格中的空格:
(2)根据上面的表格,猜想顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2(用所给的字母表达);
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.

(1)根据上面多面体模型,填写表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.
13. 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
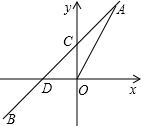 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.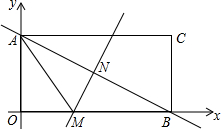 如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).
如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).