题目内容
2.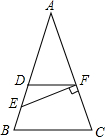 如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.
如图,等腰△ABC中,AB=AC,D是等腰AB上的一点,且AD=2DB,DF∥BC,E为DB的中点,若EF⊥AC,BC=6,则四边形DBCF的面积为15.
分析 过D点作DG⊥AC,垂足为G,过A点作AH⊥BC,垂足为H,根据题意设BE=DE=x,则AD=AF=4x,由DG∥EF,利用平行线分线段成比例求FG,由DF∥BC得△ADF∽△ABC,利用相似比求DF,同时可得∠DFG=∠C,易证Rt△DFG∽Rt△ACH,利用相似比求x,在Rt△ABH中,用勾股定理求AH,计算△ABC的面积,由△ADF∽△ABC,利用相似三角形的性质求△ADF的面积,作差求四边形DBCF的面积.
解答 解:如图,过D点作DG⊥AC,垂足为G,过A点作AH⊥BC,垂足为H,
∵E为BD的中点,且AD=2DB,
∴可设BE=DE=x,则AD=AF=4x,
∵DG⊥AC,EF⊥AC,
∴DG∥EF,
$\frac{AE}{AF}=\frac{DE}{FG}$,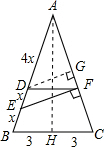
即$\frac{5x}{4x}=\frac{x}{FG}$,
解得FG=$\frac{4}{5}$x,
∵DF∥BC,
∴△ADF∽△ABC,
$\frac{DF}{BC}=\frac{AD}{AB}$,
即$\frac{DF}{6}=\frac{4x}{6x}$,
解得DF=4,
又∵DF∥BC,
∴∠DFG=∠C,
∴Rt△DFG∽Rt△ACH,
∴$\frac{DF}{AC}=\frac{FG}{CH}$,
即$\frac{4}{6x}=\frac{\frac{4x}{5}}{3}$
解得x2=2.5,
在Rt△ABH中,由勾股定理,得AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=9,
则S△ABC=$\frac{1}{2}$×BC×AH=$\frac{1}{2}$×6×9=27,
又∵△ADF∽△ABC,
∴$\frac{{S}_{△ADF}}{S△ABC}$=$\frac{4}{9}$,
S△ADF=$\frac{4}{9}$×27=12,
∴S四边形DBCF=S△ABC-S△ADF=27-12=15,
故答案为:15.
点评 本题考查了相似三角形的判定与性质,等腰三角形的性质,勾股定理.关键是通过作辅助线,构造相似三角形,利用相似比解题.

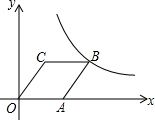 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | 2+$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
| A. | 12+2s | B. | 10+2(s+1) | C. | 12+2s-3.5 | D. | 12+2(s-3.5) |
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
| A. | 圆内 | B. | 圆上 | C. | 圆外 | D. | 都有可能 |
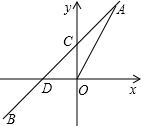 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
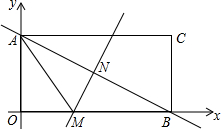 如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).
如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).