题目内容
4. 如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为$\frac{3}{2}$秒时,求此时四边形ADEC的周长是多少?
分析 (1)连接CD交AE于F,根据平行四边形的性质得到CF=DP,OF=PF,根据题意得到AF=EF,又CF=DP,根据平行四边形的判定定理证明即可;
(2)根据题意计算出OC、OP的长,根据勾股定理求出AC、CE,根据平行四边形的周长公式计算即可.
解答 (1)证明:连接CD交AE于F, ∵四边形PCOD是平行四边形,
∵四边形PCOD是平行四边形,
∴CF=DF,OF=PF,
∵PE=AO,
∴AF=EF,又CF=DP,
∴四边形ADEC为平行四边形;
(2)解:当点P运动的时间为$\frac{3}{2}$秒时,OP=$\frac{3}{2}$,OC=3,
则OE=$\frac{9}{2}$,
由勾股定理得,AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=3$\sqrt{2}$,
CE=$\sqrt{O{C}^{2}+O{E}^{2}}$=$\frac{3}{2}\sqrt{13}$,
∵四边形ADEC为平行四边形,
∴周长为(3$\sqrt{2}$+$\frac{3}{2}\sqrt{13}$)×2=6$\sqrt{2}$+3$\sqrt{13}$.
点评 本题考查的是平行四边形的性质和判定、勾股定理的应用,掌握对角线互相平分的四边形是平行四边形是解题的关键,注意坐标与图形的关系的应用.

练习册系列答案
相关题目
16.下列关系式中:①y=2x;$②\frac{y}{x}=5$;③y=-$\frac{7}{x}$;④y=5x+1;⑤y=x2-1;⑥y=$\frac{1}{{x}^{2}}$;⑦xy=11,y是x的反比例函数的共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.三角形中,三个内角的比为1:3:6,它的三个外角的比为( )
| A. | 1:3:6 | B. | 6:3:1 | C. | 9:7:4 | D. | 4:7:9 |
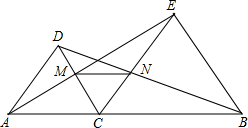 已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.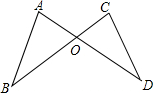 如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.
如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.