题目内容
11.已知点M(-2,3)在双曲线y=$\frac{k}{x}$上,k的值为-6.分析 直接把点M(-2,3)代入y=$\frac{k}{x}$,求出k的值即可.
解答 解:∵点M(-2,3)在双曲线y=$\frac{k}{x}$上,
∴3=$\frac{k}{-2}$,解得k=-6.
故答案为:-6.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
6.点A(-3,5)关于原点的对称点的坐标为( )
| A. | (3,5) | B. | (-3,-5) | C. | (3,-5) | D. | (5,-3) |
16.下列关系式中:①y=2x;$②\frac{y}{x}=5$;③y=-$\frac{7}{x}$;④y=5x+1;⑤y=x2-1;⑥y=$\frac{1}{{x}^{2}}$;⑦xy=11,y是x的反比例函数的共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.下列各数中,最大的数是( )
| A. | 0 | B. | -1 | C. | -2 | D. | 1 |
20.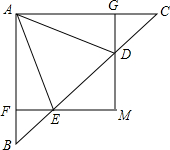 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )| A. | △CAE∽△BDA | B. | $\frac{AD}{AE}=\frac{AC}{BD}$ | C. | BD•CE=4 | D. | BE=$\sqrt{2}$BF |
1.已知点M(3,-4),那么M到原点的距离是( )
| A. | 3 | B. | 4 | C. | -4 | D. | 5 |
 四边形ABCD在平面直角坐标系中的位置如图所示,若AB⊥AD,AB∥CD,且AB=5,A点坐标为(-2,7),则B点坐标为(3,7).
四边形ABCD在平面直角坐标系中的位置如图所示,若AB⊥AD,AB∥CD,且AB=5,A点坐标为(-2,7),则B点坐标为(3,7).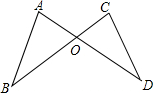 如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.
如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.