题目内容
6. 如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,求AD的长与四边形ABCD的面积.
如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,求AD的长与四边形ABCD的面积.
分析 延长AD、BC交于E,根据直角三角形两锐角互余求出∠E=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AE、CE,再利用勾股定理列式求出BE、DE,于是根据AD=AE-DE可求出AD的长,然后根据四边形ABCD的面积=Rt△ABE的面积-Rt△CDE面积列式计算即可得解.
解答 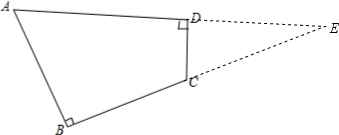 解:如图,延长AD、BC交于E.
解:如图,延长AD、BC交于E.
∵∠B=90°,∠A=60°,
∴∠E=90°-60°=30°,
在Rt△ABE和Rt△CDE中,∵AB=2,CD=1,
∴AE=2AB=2×2=4,CE=2CD=2×1=2,
由勾股定理得,BE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
DE=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AD=AE-DE=4-$\sqrt{3}$,
∴S四边形ABCD=$\frac{1}{2}$×2$\sqrt{3}$×2-$\frac{1}{2}$×$\sqrt{3}$×1=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了勾股定理的运用、直角三角形30°角所对的直角边等于斜边的一半的性质以及三角形的面积公式的运用,作辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
11.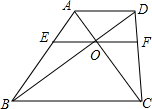 如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )
如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )
 如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )
如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )| A. | OE=OF | B. | OE≠OF | C. | OE>OF | D. | OE<OF |
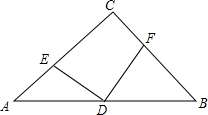 如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF.
如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF. 八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A?
八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A?