题目内容
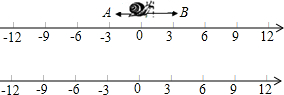
3.如图,一只蜗牛A从原点出发向数轴负方向运动,同时另一只蜗牛B也从原点出发向数轴正方向运动,已知蜗牛A的速度为1个单位长度/秒,蜗牛B的速度为4个单位长度/秒.(1)在数轴上(图1)标出蜗牛A、B从原点出发运动3秒时的位置;
(2)若蜗牛A、B从(1)中的位置同时向数轴负方向运动,爬行2秒时,
①两蜗牛在数轴上所处的位置所对应的数分别是多少?
②两蜗牛相距多少个单位长度?
(3)若蜗牛A、B从(1)中的位置同时向数轴负方向运动时,则爬行多少秒时B蜗牛刚好追上A蜗牛?
分析 (1)利用两蜗牛的速度得出从原点出发运动3秒后的位置;
(2)①根据(1)中所求分别得出两蜗牛在数轴上所处的位置所对应的数;
②利用A,B两蜗牛的位置得出其距离长度;
(3)根据两蜗牛相距15个单位列出方程求解即可.
解答 解:(1)∵蜗牛A的速度为1个单位长度/秒,蜗牛B的速度为4个单位长度/秒,
∴A、B从原点出发运动3秒时,蜗牛A的位置在-3,蜗牛B的位置在12,
在图上标注如下:
(2)①A蜗牛:-3-1×2=-5,
B蜗牛:12-4×2=4,
答:A蜗牛在数轴上所处位置对应的数是-5,B蜗牛在数轴上所处的位置所对应的数是4;
②4-(-5)=9.
答:两蜗牛相距9个单位长度;
(3)设y秒后蜗牛B追上蜗牛A,
依题意得,4y-y=15,
解得:y=5.
答:爬行5秒时B蜗牛刚好追上A蜗牛.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
11.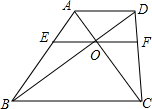 如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )
如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )
 如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )
如图.梯形ABCD中,AD∥BC,AC、BD交于点O,过点O作EF∥AD交AB、CD于点E、F,则( )| A. | OE=OF | B. | OE≠OF | C. | OE>OF | D. | OE<OF |
 实数a、b在数轴上的位置如图所示,请化简:|a-b|-2$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$.
实数a、b在数轴上的位置如图所示,请化简:|a-b|-2$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$.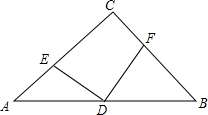 如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF.
如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF. 八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A?
八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A? 平行四边形ABCD中,AE交BC于点E,交BD于点F,且BE2=EF•EA.求证:AB2=BF•BD.
平行四边形ABCD中,AE交BC于点E,交BD于点F,且BE2=EF•EA.求证:AB2=BF•BD.
 B.
B.  C.
C.  D.
D. 