题目内容
9.如果把直角三角形的两条直角边长同时扩大到原来的3倍,那么斜边长扩大到原来的( )| A. | 3倍 | B. | 4倍 | C. | 6倍 | D. | 9倍 |
分析 设直角边分别为a与b,根据勾股定理表示出斜边c,将a,b分别换为3a与3b,即可得到斜边的变化情况.
解答 解:设直角三角形的直角边为a、b,斜边为c,
直角边扩大3倍后为3a,3b,
那么据勾股定理得原来c2=a2+b2,
现在的斜边$\sqrt{(3a)^{2}+(3b)^{2}}$=3$\sqrt{{a}^{2}+{b}^{2}}$=3c.
即斜边扩大到原来的3倍,
故选A.
点评 此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
4.一个直角三角形一直角边长为6,另一直角边长为8,则斜边长为( )
| A. | 6 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 10 |
18.现有A、B两种商品,买3件A商品和2件B商品用了160元,买2件A商品和3件B商品用了190元.如果准备购买A、B两种商品共10件,下列方案中费用最低的为( )
| A. | A商品7件和B商品3件 | B. | A商品6件和B商品4件 | ||
| C. | A商品5件和B商品5件 | D. | A商品4件和B商品6件 |
19.若a>b,则下列式子正确的是( )
| A. | -3a>-3b | B. | a-3>b-3 | C. | $\frac{3-a}{2}$>$\frac{3-b}{2}$ | D. | a+3b<4b |
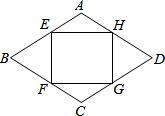 已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.
已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.