题目内容
7.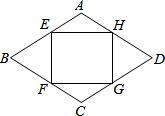 已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.
已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.
分析 首先利用菱形的性质得到∠A=∠C,∠B=∠D,AB=BC=CD=DA,然后根据AE=AH=CF=CG,得到BE=BF=DH=DG,从而证得△AEH≌△CGF,△BEF≌△DGH,证得四边形EFGH是平行四边形,然后利用有一个角是直角的平行四边形是矩形判定四边形EFGH是矩形.
解答 证明:∵四边形ABCD是菱形,
∴∠A=∠C,∠B=∠D,AB=BC=CD=DA
∵AE=AH=CF=CG,
∴BE=BF=DH=DG,
∴△AEH≌△CGF,△BEF≌△DGH,
∴EH=FG,EF=GH,
∴四边形EFGH是平行四边形,
∵∠A+∠D=180°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形EFGH是矩形.
点评 本题考查了矩形的判定,本题应用了有一个角是直角的平行四边形是矩形判定四边形EFGH是矩形,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.“今有鸡兔同笼,上有24头,下有74足,问鸡兔各几何?”设鸡有x只,兔有y只,则下列方程组中正确的是( )
| A. | $\left\{\begin{array}{l}{x-y=24}\\{2x+4y=74}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=24}\\{4x+2y=74}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=24}\\{2x+4y=74}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=24}\\{4x+2y=74}\end{array}\right.$ |
19.某班50名学生的一次安全知识竞赛成绩分布如表所示(满分10分)
这次安全知识竞赛成绩的众数是( )
| 成绩(分) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(人) | 0 | 0 | 0 | 1 | 0 | 1 | 3 | 5 | 6 | 19 | 15 |
| A. | 5分 | B. | 6分 | C. | 9分 | D. | 10分 |
9.如果把直角三角形的两条直角边长同时扩大到原来的3倍,那么斜边长扩大到原来的( )
| A. | 3倍 | B. | 4倍 | C. | 6倍 | D. | 9倍 |