题目内容
8.观察下列各式,解答问题:第1个等式:22-12=2×1+1=3;
第2个等式:32-22=2×2+1=5;
第3个等式:42-32=2×3+1=7;
第4个等式:52-42=2×4+1;
…
第n个等式:(n+1)2-n2=2n+1.(n为整数,且n≥1)
(1)根据以上规律,在上边横线上写出第4个等式和第n个等式,并说明第n个等式成立;
(2)请从下面的A,B两题中任选一道题解答,我选择A或B题.
A.利用以上规律,计算20012-20002的值.
B.利用以上规律,求3+5+7+…+1999的值.
分析 (1)根据规律写出结果即可.
(2)A:利用规律直接结果即可.
B:逆用规律即可解决问题.
解答 解:(1)52-42=2×4+1=9,
(n+1)2-n2=2n+1.
故答案分别为52-42=2×4+1=9,(n+1)2-n2=2n+1.
证明:左边=n2+2n+1-n2=2n+1.
右边=2n+1,
∴左边=右边.
∴结论成立.
(2)A:20012-20002=2×2000+1=4001.
B:3+5+7+…+1999=22-12+32-22+42-32+…+($\frac{1999+1}{2}$)2-($\frac{1991-1}{2}$)2=10002-1=999999.
点评 本题考查规律型:数字的变化类,解题的关键是掌握从一般到特殊的探究方法,找到规律,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 图1是一个水平摆放的小正方体木块,图2图3是由这样的小正方体木块按一定的规律叠放而成,其中图1有1个正方体.图2有6个正方体,图3有15个正方体,按照这样的规律继续叠放下去,则图6有正方体( )
图1是一个水平摆放的小正方体木块,图2图3是由这样的小正方体木块按一定的规律叠放而成,其中图1有1个正方体.图2有6个正方体,图3有15个正方体,按照这样的规律继续叠放下去,则图6有正方体( )
 图1是一个水平摆放的小正方体木块,图2图3是由这样的小正方体木块按一定的规律叠放而成,其中图1有1个正方体.图2有6个正方体,图3有15个正方体,按照这样的规律继续叠放下去,则图6有正方体( )
图1是一个水平摆放的小正方体木块,图2图3是由这样的小正方体木块按一定的规律叠放而成,其中图1有1个正方体.图2有6个正方体,图3有15个正方体,按照这样的规律继续叠放下去,则图6有正方体( )| A. | 45个 | B. | 60个 | C. | 66个 | D. | 84个 |
20.如图,是用棋子摆成的“上”字:如果按照此规律继续摆下去,那么通过观察,可以发现:第10个“上”字需用多少枚棋子( )
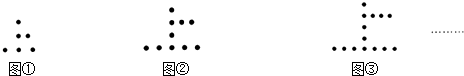
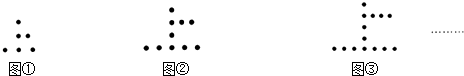
| A. | 36 | B. | 38 | C. | 42 | D. | 50 |
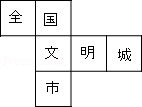 在市委、市府的领导下,全市人民齐心协力,将我市成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“全”字所在的面相对的字应是( )
在市委、市府的领导下,全市人民齐心协力,将我市成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“全”字所在的面相对的字应是( ) 李祥用棋子摆出了四个不同的图案(如图),请你仔细观察其中的规律,然后画出按此规律排列的第五个图案,看一看第五个图案中一共有多少个棋子,你能归纳出一个一般性的结论吗?
李祥用棋子摆出了四个不同的图案(如图),请你仔细观察其中的规律,然后画出按此规律排列的第五个图案,看一看第五个图案中一共有多少个棋子,你能归纳出一个一般性的结论吗?