题目内容
13.用配方法解下列方程:(1)9y2-18y-4=0
(2)x2+3=2$\sqrt{3}$x.
分析 (1)第一步移项,把常数项移到右边;第二步将二次项系数化为1;第三步配方,左右两边加上一次项系数一半的平方;第四步左边写成完全平方式;第五步,直接开方即可;
(2)将一次项移至左边,再根据公式写成完全平方式,最后开方可得.
解答 解:(1)∵9y2-18y-4=0
∴9y2-18y=4,
∴y2-2y=$\frac{4}{9}$,
∴(y-1)2=$\frac{4}{9}$+1,即(y-1)2=$\frac{13}{9}$,
∴y-1=±$\frac{\sqrt{13}}{3}$,
∴y1=$\frac{3+\sqrt{13}}{3}$,y2=$\frac{3-\sqrt{13}}{3}$;
(2)由x2+3=2$\sqrt{3}$x可得x2-2$\sqrt{3}$x+3=0,
∴(x-$\sqrt{3}$)2=0,
∴x=$\sqrt{3}$.
点评 此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用,把左边配成完全平方式,右边化为常数.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
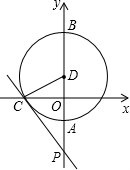 如图⊙D交y轴于A、B两点,交x轴于点C,已知点D的坐标为(0,1),过点C的直线$y=-2\sqrt{2}x-8$与y轴交于点P.
如图⊙D交y轴于A、B两点,交x轴于点C,已知点D的坐标为(0,1),过点C的直线$y=-2\sqrt{2}x-8$与y轴交于点P.