题目内容
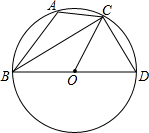 如图,△ABC内接于⊙O,BD是⊙O的直径,∠A=120°,CD=3cm,求扇形BOC的面积.
如图,△ABC内接于⊙O,BD是⊙O的直径,∠A=120°,CD=3cm,求扇形BOC的面积.考点:扇形面积的计算
专题:
分析:先根据圆内接四边形的性质求出∠D的度数,再由圆周角定理求出∠BOC的度数,根据扇形的面积公式求出扇形的面积即可.
解答:解:∵四边形ABCD是圆内接四边形,∠A=120°,
∴∠D=180°-120°=60°,
∵OD=OC,
∴△OCD是等边三角形,
∴OC=OD=3cm.
∴∠BOC=2∠D=120°.
∴S扇形BOC=
=3π.
∴∠D=180°-120°=60°,
∵OD=OC,
∴△OCD是等边三角形,
∴OC=OD=3cm.
∴∠BOC=2∠D=120°.
∴S扇形BOC=
| 120π×32 |
| 360 |
点评:本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列计算或化简正确的是( )
A、2
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
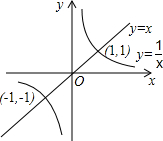 我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>
我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>| 1 |
| x |
| A、x>1 |
| B、-1<x<0 |
| C、x>1或-1<x<0 |
| D、以上都不对 |
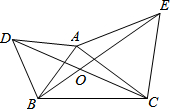 如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是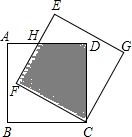 如图,边长为3的正方形ABCD终点C按顺时针旋转30°,得到正方形EFCG,交AD于点H,则阴影部分的面积为
如图,边长为3的正方形ABCD终点C按顺时针旋转30°,得到正方形EFCG,交AD于点H,则阴影部分的面积为 (1)将半圆绕它的直径旋转一周形成的几何体是
(1)将半圆绕它的直径旋转一周形成的几何体是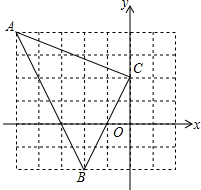 已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.
已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.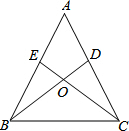 已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.求证:(1)OB=OC;(2)BE=CD.
已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.求证:(1)OB=OC;(2)BE=CD.