题目内容
如图:AB∥CD
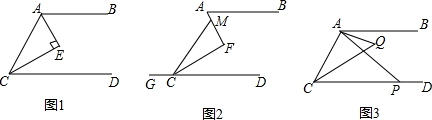
(1)若AE平分∠BAC,∠CAE+∠ACE=90°,求证:CE平分∠ACD;
(2)AF⊥CF,M是AF上一点,且∠MCF=∠FCD,试问∠BAF和∠MCG之间有怎样的数量关系,写出其数量关系式并说明理由;
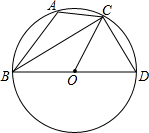
(3)P是CD上一点,∠ACP的平分线和∠BAP的平分线交于Q,若∠CAP=80°.求∠Q的度数.

(1)若AE平分∠BAC,∠CAE+∠ACE=90°,求证:CE平分∠ACD;
(2)AF⊥CF,M是AF上一点,且∠MCF=∠FCD,试问∠BAF和∠MCG之间有怎样的数量关系,写出其数量关系式并说明理由;
(3)P是CD上一点,∠ACP的平分线和∠BAP的平分线交于Q,若∠CAP=80°.求∠Q的度数.
考点:平行线的性质
专题:
分析:(1)根据角平分线的定义可得∠CAE=∠BAE,再根据平行线的性质可得∠BAC+∠ACD=180°,再由条件∠CAE+∠ACE=90°可得∠BAE+∠ECD=90°,然后根据等式的性质可得结论;
(2)首先过F作EF∥AB,然后判定AB∥CD∥EF,根据平行线的性质可得∠A=∠EFA,∠FCD=∠EFC,进而得到∠FCD=90°-∠A,再根据邻补角的性质街和等量代换可得
∠GCM=180°-2∠FCD=180°-2(90°-∠A)=2∠A;
(3)根据角平分线的性质可得∠1=∠2=
∠BAP,∠3=∠4=
∠ACP,再根据平行线的性质可得∠BAP+∠ACP=100°,进而可得∠1+∠3=50°,然后再利用三角形内角和定理可得答案.
(2)首先过F作EF∥AB,然后判定AB∥CD∥EF,根据平行线的性质可得∠A=∠EFA,∠FCD=∠EFC,进而得到∠FCD=90°-∠A,再根据邻补角的性质街和等量代换可得
∠GCM=180°-2∠FCD=180°-2(90°-∠A)=2∠A;
(3)根据角平分线的性质可得∠1=∠2=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:∵AE平分∠BAC,
∴∠CAE=∠BAE=
∠CAB,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠CAE+∠ACE=90°,
∴∠BAE+∠ECD=90°,
∵∠CAE=∠BAE,
∴∠ACE=∠ECD,
∴CE平分∠ACD;
(2)∠MCG=2∠A;
理由:过F作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A=∠EFA,∠FCD=∠EFC,
∵AF⊥CF,
∴∠AFC=90°,
∴∠A+∠FCD=90°,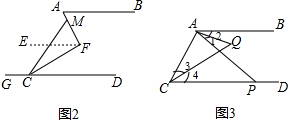
∴∠FCD=90°-∠A,
∵∠GCM=180°-∠MCD,∠MCF=∠FCD,
∴∠GCM=180°-2∠FCD=180°-2(90°-∠A)=2∠A.
(3)∵∠ACP的平分线和∠BAP的平分线交于Q,
∴∠1=∠2=
∠BAP,∠3=∠4=
∠ACP,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠CAP=80°,
∴∠BAP+∠ACP=100°,
∴∠1+∠3=50°,
∴∠Q=180°-80°-50°=50°.
∴∠CAE=∠BAE=
| 1 |
| 2 |
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠CAE+∠ACE=90°,
∴∠BAE+∠ECD=90°,
∵∠CAE=∠BAE,
∴∠ACE=∠ECD,
∴CE平分∠ACD;
(2)∠MCG=2∠A;
理由:过F作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A=∠EFA,∠FCD=∠EFC,
∵AF⊥CF,
∴∠AFC=90°,
∴∠A+∠FCD=90°,

∴∠FCD=90°-∠A,
∵∠GCM=180°-∠MCD,∠MCF=∠FCD,
∴∠GCM=180°-2∠FCD=180°-2(90°-∠A)=2∠A.
(3)∵∠ACP的平分线和∠BAP的平分线交于Q,
∴∠1=∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠CAP=80°,
∴∠BAP+∠ACP=100°,
∴∠1+∠3=50°,
∴∠Q=180°-80°-50°=50°.
点评:此题主要考查了平行线的性质,角平分线定义,三角形内角和定理,关键是正确理清角之间的和差关系.

练习册系列答案
相关题目
 如图,△ABC内接于⊙O,BD是⊙O的直径,∠A=120°,CD=3cm,求扇形BOC的面积.
如图,△ABC内接于⊙O,BD是⊙O的直径,∠A=120°,CD=3cm,求扇形BOC的面积. 如图,∠ABC=∠BAD=90°,点E,F分别是AC,BC的中点.
如图,∠ABC=∠BAD=90°,点E,F分别是AC,BC的中点.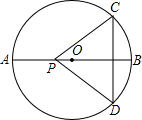 如图,已知:⊙O中AB是直径,点P在AB上,PB平分∠CPD,求证:PC=PD.
如图,已知:⊙O中AB是直径,点P在AB上,PB平分∠CPD,求证:PC=PD. 如图,AB=AC,AD是∠EAC的平分线,AD∥BC,∠B=64°,求∠EAD、∠DAC、∠C的度数.
如图,AB=AC,AD是∠EAC的平分线,AD∥BC,∠B=64°,求∠EAD、∠DAC、∠C的度数. 如图,△ABC中,∠C=90°,∠A=30°,已知AC=3,求周长.
如图,△ABC中,∠C=90°,∠A=30°,已知AC=3,求周长. 如图,AB∥CD,直线EF分别交AB、CD分于点E、F,FH平分∠EFD,若∠1=110°,则∠2=
如图,AB∥CD,直线EF分别交AB、CD分于点E、F,FH平分∠EFD,若∠1=110°,则∠2=