题目内容
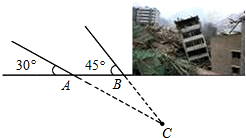 某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3m,探测线与地面的夹角分别是35°和45°,试确定生命所在点C的深度.(参考数据:
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3m,探测线与地面的夹角分别是35°和45°,试确定生命所在点C的深度.(参考数据:| 2 |
| 3 |
考点:解直角三角形的应用
专题:
分析:首先分析图形:根据题意构造直角三角形;本题涉多个直角三角形,应利用其公共边构造关系式,进而可求出答案.
解答: 解:如图,过点C作CH⊥AB交AB的延长线于H点.
解:如图,过点C作CH⊥AB交AB的延长线于H点.
∵探测线与地面的夹角为35°和45°,
∴∠CAH=30°∠CBH=45°,
设CH=x,则BH=x米,
在Rt△AHC中,
=tan∠BAC,
即:tan35°=
≈0.7,
解得:x=7.
答:生命所在点C的深度约为7米.
 解:如图,过点C作CH⊥AB交AB的延长线于H点.
解:如图,过点C作CH⊥AB交AB的延长线于H点.∵探测线与地面的夹角为35°和45°,
∴∠CAH=30°∠CBH=45°,
设CH=x,则BH=x米,
在Rt△AHC中,
| CH |
| AH |
即:tan35°=
| x |
| x+3 |
解得:x=7.
答:生命所在点C的深度约为7米.
点评:考查了解直角三角形的应用,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目




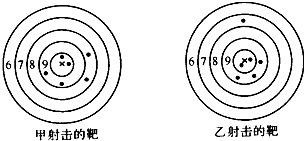 如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲,乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.