题目内容
8. 如图,已知点B的坐标为(10,0),点P(t,0)是OB上的一个动点,在x轴上方作等边△OPE和△BPF,连接EF,G为EF的中点.
如图,已知点B的坐标为(10,0),点P(t,0)是OB上的一个动点,在x轴上方作等边△OPE和△BPF,连接EF,G为EF的中点.(1)当t=5时,EF∥OB;
(2)双曲线y=$\frac{k}{x}$过点G,PG=$\frac{\sqrt{79}}{2}$时,则k=10$\sqrt{3}$或15$\sqrt{3}$.
分析 (1)作EM⊥OB于M点,FN⊥OB于N点,根据等边三角形的性质得EM=$\frac{\sqrt{3}}{2}$OP,FN=$\frac{\sqrt{3}}{2}$PB,所以EM=FN时,EF∥OB,则$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{2}$(10-t),然后即方程即可得到t的值;
(2)作GH⊥OB于H点,则GH为梯形EMNF的中位线,根据梯形中位线的性质得GH=$\frac{1}{2}$(EM+FN)=$\frac{5\sqrt{3}}{2}$,HM=$\frac{1}{2}$MN=$\frac{1}{2}$(ON-OM)=$\frac{5}{2}$,得到PH=$\frac{5}{2}$-$\frac{1}{2}$t或$\frac{1}{2}$t-$\frac{5}{2}$,再利用勾股定理得PG2=GH2+PH2,即($\frac{5\sqrt{3}}{2}$)2+($\frac{5-t}{2}$)2=($\frac{\sqrt{79}}{2}$)2,解得t1=3,t2=7,然后分别确定G点坐标,再代入反比例函数解析式可得到k的值.
解答 解:(1)如图,作EM⊥OB于M点,FN⊥OB于N点,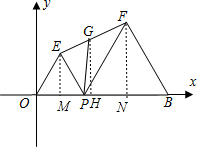
∵△OPE和△BPF都是等边三角形,
∴EM=$\frac{\sqrt{3}}{2}$OP,FN=$\frac{\sqrt{3}}{2}$PB,
当EM=FN时,EF∥OB,
∵P(t,0),B(10,0),
∴PO=t,PB=10-t
∴$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{2}$(10-t),
∴t=5;
故答案为:5.
(2)作GH⊥OB于H点,
∵G为EF的中点,
∴GH为梯形EMNF的中位线,
∴GH=$\frac{1}{2}$(EM+FN)=$\frac{1}{2}$[$\frac{\sqrt{3}}{2}$t+$\frac{\sqrt{3}}{2}$(10-t)]=$\frac{5\sqrt{3}}{2}$,HM=$\frac{1}{2}$MN=$\frac{1}{2}$(ON-OM)=$\frac{1}{2}$[t+$\frac{1}{2}$(10-t)-$\frac{1}{2}$t]=$\frac{5}{2}$,
∴PH=$\frac{5}{2}$-$\frac{1}{2}$t或$\frac{1}{2}$t-$\frac{5}{2}$,
在Rt△PGH中,PG2=GH2+PH2,
∴($\frac{5\sqrt{3}}{2}$)2+($\frac{5-t}{2}$)2=($\frac{\sqrt{79}}{2}$)2,
∴t1=3,t2=7,
当t=3时,OH=$\frac{5}{2}$+$\frac{1}{2}$t=4,
∴G点坐标为(4,$\frac{5\sqrt{3}}{2}$),
把G(4,$\frac{5\sqrt{3}}{2}$)代入y=$\frac{k}{x}$得k=4×$\frac{5\sqrt{3}}{2}$=10$\sqrt{3}$;
当t=7时,OH=$\frac{5}{2}$+$\frac{t}{2}$=6,
∴G点坐标为(6,$\frac{5\sqrt{3}}{2}$),
把G(6,$\frac{5\sqrt{3}}{2}$)代入y=$\frac{k}{x}$得k=6×$\frac{5\sqrt{3}}{2}$=15$\sqrt{3}$;
∴k的值为10$\sqrt{3}$或15$\sqrt{3}$.
故答案为:10$\sqrt{3}$或15$\sqrt{3}$.
点评 本题考查了反比例函数的综合题:反比例函数图象上点的坐标满足其函数解析式,运用待定系数法求函数的解析式;掌握等边三角形的性质、含30°的直角三角形三边的关系和勾股定理.

| A. | 3x-2 | B. | 3x-1=8 | C. | 4x+y=3 | D. | $\frac{1}{2}$x-3>1 |
| A. | 由x+2=0得x=2 | B. | 由$\frac{1}{3}$x=0得x=3 | C. | 由-2x=-1得x=-$\frac{1}{2}$ | D. | 由2=x-3得x=5 |
| A. | 矩形的对角线互相平分且相等 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 正方形的对角线互相垂直平分 | |
| D. | 等腰三角形底边上的中点到两腰的距离相等 |
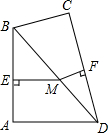 如图所示,在四边形ABCD中,∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,求证:$\frac{MF}{BC}$+$\frac{ME}{AD}$=1.
如图所示,在四边形ABCD中,∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,求证:$\frac{MF}{BC}$+$\frac{ME}{AD}$=1. 在一次自行车越野赛中,出发mh后,小明骑行了25km,小刚骑行了18km,此后两人分别以akm/h,bkm/h匀速骑行,他们骑行的时间t(单位:h)与骑行的路程s(单位:km)之间的函数关系如图,观察图象,下列说法:
在一次自行车越野赛中,出发mh后,小明骑行了25km,小刚骑行了18km,此后两人分别以akm/h,bkm/h匀速骑行,他们骑行的时间t(单位:h)与骑行的路程s(单位:km)之间的函数关系如图,观察图象,下列说法: 二次函数 y=x2+bx+c的图象经过点(1,0),(3,0).
二次函数 y=x2+bx+c的图象经过点(1,0),(3,0).